ANELLIPTIC ANISOTROPY

The extended Stolt algorithm is applied to the case of anelliptic anisotropy. Anelliptic anisotropy is an extension of elliptic anisotropy that retains the convenient symmetry properties of the elliptic anisotropy in approximation. Muir and Dellinger 1985 showed that the equations for elliptic anisotropy of the form

$$f = (z-{\rm term})^2 + (x-{\rm term})^2$$ (5)

can be generalized by adding an anelliptic factor q:  

$$f = {{z^4+(1+q) z^2 x^2 +x^4}\over{z^2 + x^2}}$$ (6)

The anelliptic factor q gives the deviation of true horizontal velocity and paraxial (near vertical, short spread) NMO velocity and perturbs the behavior away from ellipticity in between the coordinate axes. q=1 reduces equation (6) back into the elliptic form. The dispersion relation for the anelliptic case is given by  

$$\omega^2 = {{(v_z^2 k_z^2)^2+(1+q)v_z^2 k_z^2 v_x^2 k_x^2 + (v_x^2 k_x^2)^2} \over{v_z^2 k_z^2 + v_x^2 k_x^2}}$$ (7)

Using again the relation

$$k_\tau = v_z k_z$$

equation (7) becomes  

$$\omega^2 = {{k_\tau^4 + (1+q)v_x^2 k_x^2 k_\tau^2 + (v_x^2 k_x^2)^2} \over {k_\tau^2 + v_x^2 k_x^2}}$$ (8)

It is obvious that the transformation into the time domain removes any dependence of the unknown vertical velocity in the dispersion relation. It is now a function of parameters that can all be measured on the surface. Equation (8) can be transformed to  

$$k_\tau^2 = - {{(1+q)v_x^2-w^2}\over{2}}+ {1\over2}\sqrt{(4-(2(1+q))w^2 v_x^2 k_x^2 + ((1+q)^2 -4 )v_x^4 k_x^4 + w^4 }$$ (9)

The Jacobian for the Stolt migration is given by  

$${\partial \omega \over \partial k_\tau} = {1\over 2}+\sqrt{{... ...x^4 k_x^4)}\over{k_\tau^4+2 k_\tau^2 v_x^2 k_x^2 +v_x^4 k_x^4}}$$ (10)

Setting q=1 results in the well-known Jacobian for the elliptic case.

After implementation of the dispersion relation and Jacobian in the Stolt migration algorithm, the effect of different q values is tested on an input consisting of three spikes. The result can be seen in Figure .

 

stolt
Figure 1 Impulse responses of the Stolt migration for different values of anelliptic anisotropy. Click the button to see a resulting movie

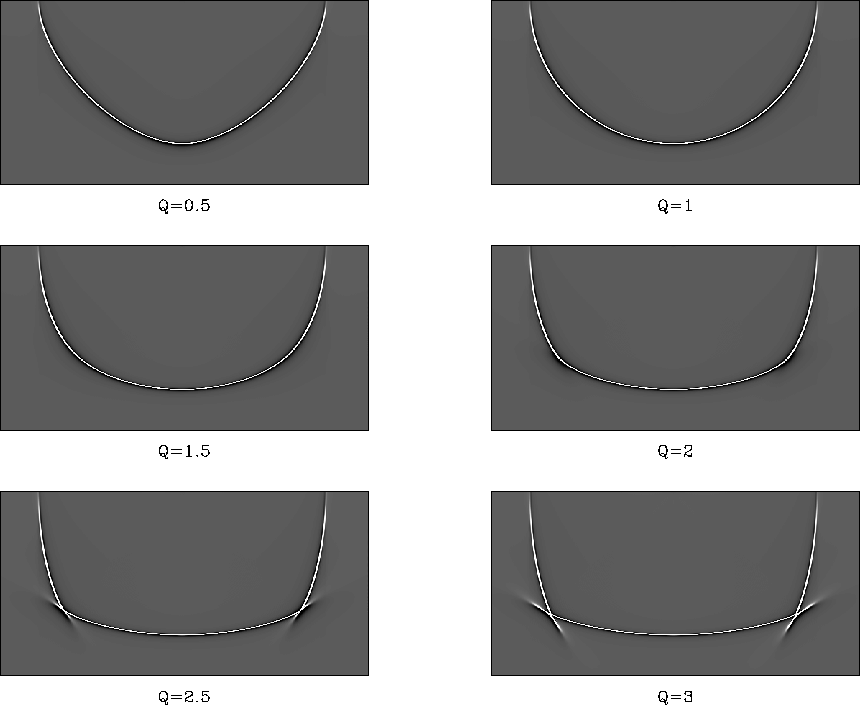Going from q=0.5 to q=3, the effect of the anisotropy can be clearly observed. The v-shaped impulse response at q=0.5 becomes an ellipse for q=1 and changes slowly into triplications for larger q values. The triplications result from extreme velocity variations in different directions. This triplicating behavior is shown in more detail for q=4 in Figure .

 

stolt4
Figure 2 Migration result for q=4

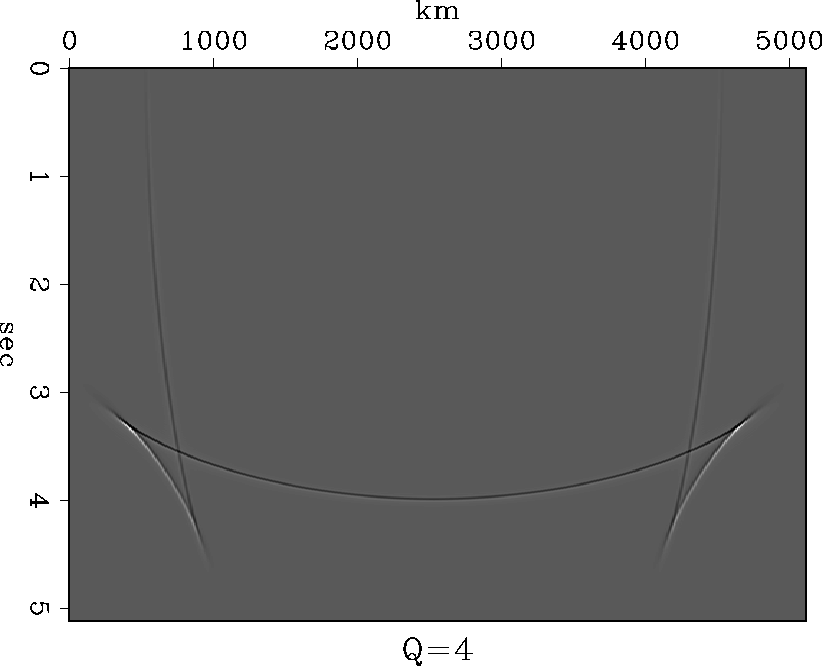Most of the energy is concentrated in the triplications and along the apex of the semi-circle. It diminishes along the sides of the semi-circle.