




Next: NON-PARALLEL FEATURES OF INTERPOLATION
Up: Blondel & Muir: Parallel
Previous: INTRODUCTION
At any angular frequency 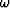 , the Fourier transform of a discrete,
regular function of time is given by the following summation:
, the Fourier transform of a discrete,
regular function of time is given by the following summation:
| 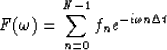 |
(1) |
where N is the number of time samples, 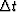 is the time sampling
rate, and fn is the discrete signal. We notice that
equation (1) relates a discrete signal to its continuous
Fourier transform. This expression can also be interpreted as a dot
product between the discrete time function and a vector of powers
of exponentials that depend on the particular frequency
is the time sampling
rate, and fn is the discrete signal. We notice that
equation (1) relates a discrete signal to its continuous
Fourier transform. This expression can also be interpreted as a dot
product between the discrete time function and a vector of powers
of exponentials that depend on the particular frequency 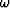 .Then, for a set of frequencies
.Then, for a set of frequencies 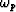 , the estimates of the
Fourier transform result from a matrix multiplication with the discrete
time function.
, the estimates of the
Fourier transform result from a matrix multiplication with the discrete
time function.
The implementation of this method is straightforward. The calculation
of the matrix of exponentials is coded in parallel, for all frequencies
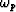 . A built-in function of Fortran 90 performs an efficient
vector-matrix multiplication directly yielding the remapped frequency
domain.
. A built-in function of Fortran 90 performs an efficient
vector-matrix multiplication directly yielding the remapped frequency
domain.





Next: NON-PARALLEL FEATURES OF INTERPOLATION
Up: Blondel & Muir: Parallel
Previous: INTRODUCTION
Stanford Exploration Project
11/16/1997
![]() , the Fourier transform of a discrete,
regular function of time is given by the following summation:
, the Fourier transform of a discrete,
regular function of time is given by the following summation:
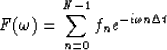
![]() . A built-in function of Fortran 90 performs an efficient
vector-matrix multiplication directly yielding the remapped frequency
domain.
. A built-in function of Fortran 90 performs an efficient
vector-matrix multiplication directly yielding the remapped frequency
domain.