




Next: Nearest-neighbor interpolation
Up: Lin, Teng, & Muir:
Previous: INTRODUCTION
The formula for Stolt migration is
| ![\begin{displaymath}
model(x,z)=2DFT^{-1}\{data[k_x,\omega(k_x,k_z) ] \frac{d\omega}
{dk_z}\}\end{displaymath}](img1.gif) |
(1) |
We first Fourier transform the data set in the (t,x) domain into
the 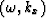 domain, then map
domain, then map 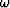 into kz by the dispersion
relation as follows:
into kz by the dispersion
relation as follows:
| 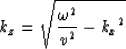 |
(2) |
In this mapping step, we need to use an interpolation operator
because of the discrete Fourier transform.
Finally, we inverse Fourier transform the data in the (kz,kx) domain back to
the (z,x) domain.
To compare the five interpolation methods, we implement them
in a Stolt migration of three impulses at different depths
in anelliptic anisotropy media Dellinger et al. (1993), which causes
triplication at the corners of each impulse response.
We use the same synthetic data and parameters for each
interpolation method in order to compare the results of different interpolators.





Next: Nearest-neighbor interpolation
Up: Lin, Teng, & Muir:
Previous: INTRODUCTION
Stanford Exploration Project
11/16/1997