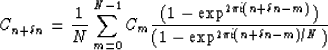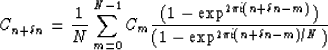Muir's interpolation

To do more precise interpolation in the frequency-domain, Francis Muir derived the following equation:

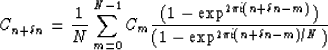$$C_{n+ \delta n}=\frac{1}{N}\sum_{m=0}^{N-1}C_{m}\frac{(1-\exp^{2\pi i(n+\delta n-m)})}{(1-\exp^{2\pi i(n+\delta n-m)/N})}$$ (6)

This formula is equivalent to the slow Fourier Transform (SFT) but is implemented in the frequency domain. The method provides a fast model of SFT with exact interpolation.

Muir's interpolator shows a perfect impulse response without any artifacts in Figure 5.