




Next: DSR artifacts
Up: OFFSET SEPARATION
Previous: Migration for a single
Another way to greatly improve the speed of the algorithm is to process
all the constant-offset sections at the same time.
In this case the phase loop can be computed
once for all the offsets.
The need to keep the constant-offset sections separated
is accomplished by observing that
the DSR equation can be rewritten in an offset separable form
| 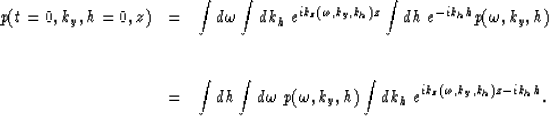 |
(7) |
The integral in h stacks the independently prestack migrated
constant-offset sections. As we are interested in each
constant-offset section, we rewrite
the DSR in an offset separable form
| 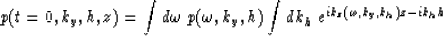 |
(8) |
and observe that the integral in kh can be replaced by a
fast Fourier transform of the exponential
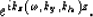
The algorithm becomes:
FFT along t,y axes  do z
do ky
do
do z
do ky
do 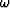 do kh
do kh
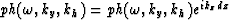
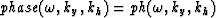 FFT phase along kh axis
FFT phase along kh axis
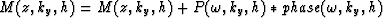
This algorithm can be executed in parallel for all the
values of 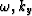 .Note that for depth variable velocity the phase is carried from one
depth level to another, corresponding to an integral in depth
of the phase terms corresponding to each depth slice.
.Note that for depth variable velocity the phase is carried from one
depth level to another, corresponding to an integral in depth
of the phase terms corresponding to each depth slice.





Next: DSR artifacts
Up: OFFSET SEPARATION
Previous: Migration for a single
Stanford Exploration Project
11/16/1997
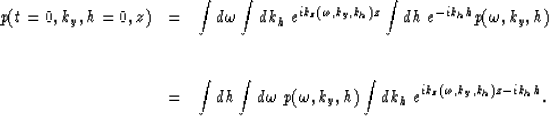
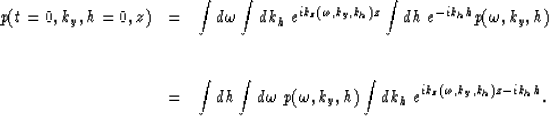
![]()
do z do ky do
do kh
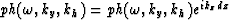
FFT phase along kh axis
![]() .Note that for depth variable velocity the phase is carried from one
depth level to another, corresponding to an integral in depth
of the phase terms corresponding to each depth slice.
.Note that for depth variable velocity the phase is carried from one
depth level to another, corresponding to an integral in depth
of the phase terms corresponding to each depth slice.