Next: About this document ...
Up: REFERENCES
Previous: REFERENCES
Downward continuation using the DSR equation for a separate
constant-offset sections requires the computation of the integral
in equation (A-1). This can be done for all offsets by
taking the inverse transform of the downward continuation
exponential, or for a single offset by finding a stationary
phase approximation to the integral
| 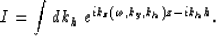 |
(10) |
Integrals of the form
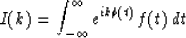
are approximated asymptotically (Zauderer, 1989) when
 by
by
![\begin{displaymath}
I(k) \approx e^{ik\phi (t_0)} f(t_0)
e^{{\rm sign} (\phi''(...
...t[{{2\pi} \over {k \mid \phi''(t_0) \mid }} \right]^{1 \over 2}\end{displaymath}](img42.gif)
where t0 is the ``stationary point'' where the derivative of
the phase is zero. The approximation described here assumes the
second derivative is non-zero, which I will prove is the situation in
this case.
The phase of the exponential in this case is
| ![\begin{displaymath}
\phi(k_h)={-{\rm sign}(\omega) z \left[ \;
\sqrt{{\omega^2 \...
...omega^2 \over v^2}-{1 \over 4}(k_y-k_h)^2} \; \right] - k_h h}.\end{displaymath}](img43.gif) |
(11) |
In order to evaluate the stationary point we need to find the
roots of the equation
| ![\begin{displaymath}
\phi ' (k_h)=
-h +{\rm sign}(\omega) z \left[ {{k_h+k_y} \ov...
...
{\sqrt{{\omega^2 \over v^2}-{1 \over 4}(k_y-k_h)^2}}} \right].\end{displaymath}](img44.gif) |
(12) |
I was not able to find these roots, as it involves an equation of
sixth degree. However, I will point out some properties of the
phase, which should make the numerical computation simpler than
the full integration.
The second derivative of the phase is non-zero, as it consists
of the sum of four positive terms
multiplied by 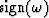 :
:
| ![\begin{displaymath}
\begin{array}
{lcl}
\phi '' (k_h) & = &
{{{\rm sign}(\omega...
...\over 4}(k_y+k_h)^2} \right ]^{3 \over 2}}} \right].\end{array}\end{displaymath}](img46.gif) |
(13) |
This ensures that there is no change in curvature, and the phase
always has a maximum or a minimum and therefore a stationary point.
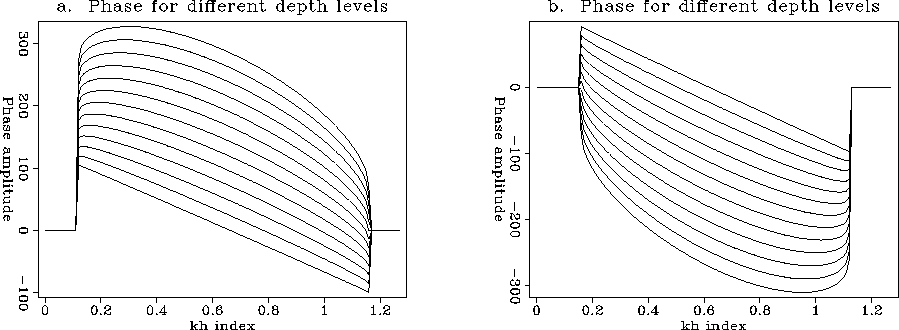
Indeed, for a fixed pair of values 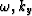 , Figure A-1
shows the phase function for several depth levels.
The sign of
, Figure A-1
shows the phase function for several depth levels.
The sign of 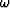 determines if the phase is positive
or negative.
App1
determines if the phase is positive
or negative.
App1
Figure 8 Plot of the phase function for a constant pair of values 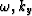 .The different plots correspond to increasing depth levels.
.The different plots correspond to increasing depth levels.
a. Phase corresponding to positive 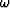 .
.
b. Phase corresponding to negative 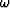 .
.










Next: About this document ...
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
11/16/1997
![]()
![]()
![\begin{displaymath}
\phi(k_h)={-{\rm sign}(\omega) z \left[ \;
\sqrt{{\omega^2 \...
...omega^2 \over v^2}-{1 \over 4}(k_y-k_h)^2} \; \right] - k_h h}.\end{displaymath}](img43.gif)
![\begin{displaymath}
\phi ' (k_h)=
-h +{\rm sign}(\omega) z \left[ {{k_h+k_y} \ov...
...
{\sqrt{{\omega^2 \over v^2}-{1 \over 4}(k_y-k_h)^2}}} \right].\end{displaymath}](img44.gif)
![]() :
:
![\begin{displaymath}
\begin{array}
{lcl}
\phi '' (k_h) & = &
{{{\rm sign}(\omega...
...\over 4}(k_y+k_h)^2} \right ]^{3 \over 2}}} \right].\end{array}\end{displaymath}](img46.gif)