Memory layout

The memory layout for processing time slices is illustrated in Figure . The time slices are local to each processor and the time axis is the parallel dimension. Thus, the number of processors needed is the number of time samples, and the memory of each processor must be large enough to load and process one time slice. When the amount of data exceeds the memory available, the process can run on lumps of data. The lumps may be pieces of data cut in the (x,y) space, preserving the parallel axis and relieving the processors memory, or they may be cut in time, shortening the parallel axis but requiring a smaller area of overlap between successive lumps.

 

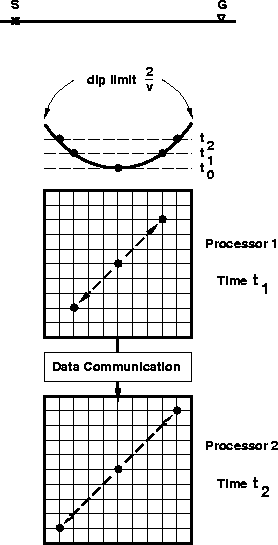
tsproc Figure 3 The top-most drawing represents the elliptic dip-limited DMO operator. I assume that the offset line bisects the x- and y- axes on the Earth's surface. Below, the two grids represent the data layout inside the processors. Each processor contains a time slice of data. Processor 1 contains the time slice at t=t0 and performs the data communication across the (x,y) space that corresponds to a vertical shift from t0 to t1. During this time, processor 2 performs the same kind of operation for a vertical shift from t1 to t2. Then, processor 1 sums its output in the output volume and communicates its input to processor 2. The action is then repeated, moving the data across the (x,y) space for a vertical shift from t0 to t2.

Unlike the previous algorithm, data communication is performed in a single direction, up the time axis, and does not depend on the offset and azimuth distribution. The long ranging and chaotic communications in the (x,y) space take place in-processor. Thus, the processing of time slices results in a more efficient inter-processor communication than the trace processing.