Load balance

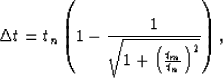
Because the DMO elliptic operator is dip-limited, it does not extend all the way up to the Earth's surface (t=0). The time spread of the impulse response is given by:  

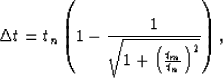$$\Delta t = t_n \left( 1 - \frac{1} {\sqrt{1+\left( \frac{t_m}{t_n} \right) ^2}} \right),$$ (1)

where t_n is the time location of the impulse in the input space, h is the half offset, v is the velocity of the medium, and t_m = 2h/v is the horizontal two-way traveltime between shot and midpoint. Figure  is a plot of the time spread as a function of NMO time.

 

magic Figure 4 Time spread of the impulse responses of DMO as a function of the impulse location, tn. The maximum time spread occurs for the input time $t_n=t_m/\protect\sqrt{G}$where G is the golden number. Click on the following button to see the curve for different times tm.

An interesting feature of these curves is that the time spread of the impulse responses never exceeds $\mu t_m$ where $\mu$ is  

$$\mu = \sqrt{G} \left( \frac{G-1}{G+1} \right) \simeq .300283... ...m{, \hspace{.3in} with \hspace{.1in}} G = \frac{1+\sqrt{5}}{2}.$$ (2)

Because t_m is limited by the maximum offset, the time spread is much shorter than the full trace length.

During the process, the time slices are shifted upward until they reach the maximum time spread. Of course, only the time slice corresponding to the maximum time spread will have to be processed all the way. Other time slices, like for example t_n=5 seconds (Figure ), will be processed for the first .1 second and then pass through idle processors. Obviously, the later time slices require less processing than the earlier ones, and thus represent a waste of processing capacity. The following formula gives the load balance as a function of trace length:  

$${\rm Load}(t_{\rm max}) = \frac{1}{t_{\rm max}} \int_0^{t_{\rm max}} \frac{\Delta t(t)}{\Delta t_{\rm max}} dt.$$ (3)

This formula is derived from the two following observations. The time for which the processors are active is proportional to the area under the curve representing $\Delta t(t)$ in Figure , $\int \Delta t(t) dt$. The total computation time is proportional to both the trace length and the maximum time shift, $t_{\rm max} \Delta t_{\rm max}$. The computer load is then the ratio of the effective working time to the total execution time, as expressed in equation (3). As an example, for a trace length of 4 seconds and a midpoint time t_m=1 second, the load balance reaches seventy percent (Figure ).

 

integ Figure 5 Load balance as a function of the trace length. The optimal load balance of eighty percent corresponds to a trace length which is a function of tm (=2h/v). The bigger tm is, the later the load balance is optimal. Click on the following button to see a movie of the load balance for different values of tm.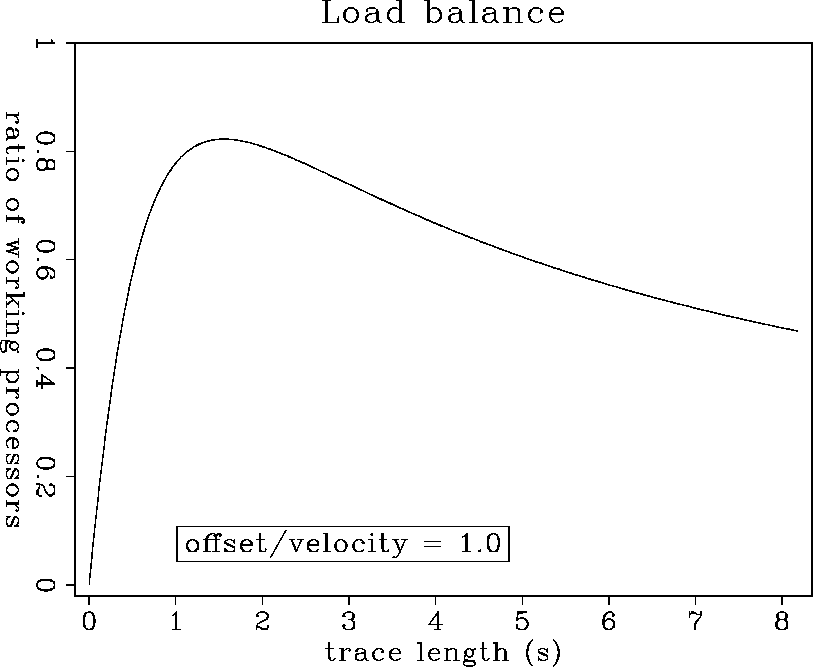

This algorithm allows a more efficient distribution of work between processors than the spiral trace processing described earlier. I implemented this algorithm for a two-dimensional model (Figure  is an output of the program) but the run time is similar to a serial implementation of DMO (in 2-D, trace processing is more straightforward than time slice spreading). However, the real advantage of the method will appear in processing 3-D land data.