Jakubowicz 1990 gave an elegant formulation of (f,k) dip moveout where a finite number of dips are processed separately and stacked according to equation (1),
| |
(1) |
| |
(2) |
In the general case of depth-variable velocity, there is no analytic
expression of the amplitude along the operator but the dip-decomposition
method gives us a qualitative idea. Indeed, the operator of variable-velocity
dip moveout may be build point by point for a range of dips regularly
sampled. Then, a region where the points are close to each other
allows a significant stack of the dipping segments of the operator, and
thus corresponds to an area of high amplitude. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an impulse response of dip moveout in a time-variable velocity model
whose profile is represented in Figure
shows an impulse response of dip moveout in a time-variable velocity model
whose profile is represented in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
|
vel
Figure 1 Interval velocity model. | 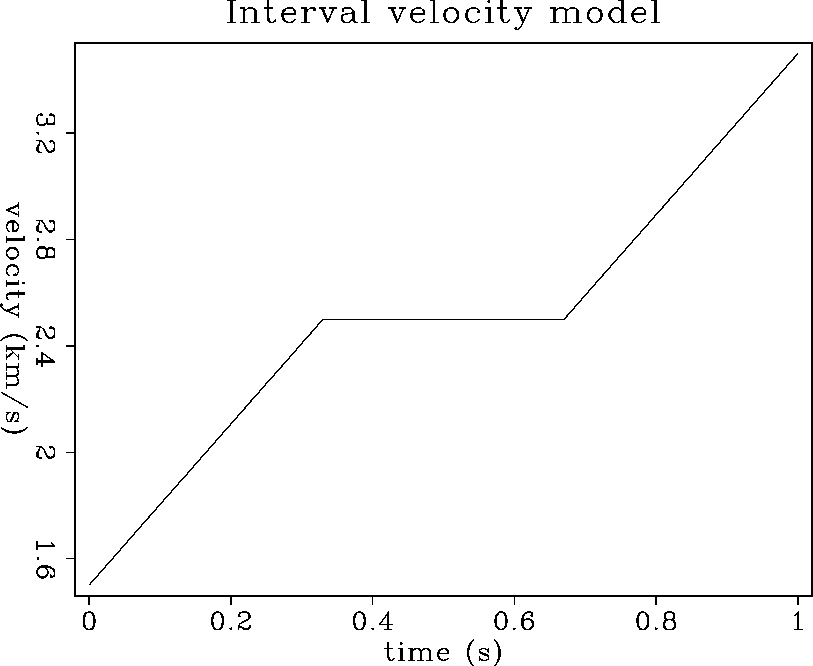 |
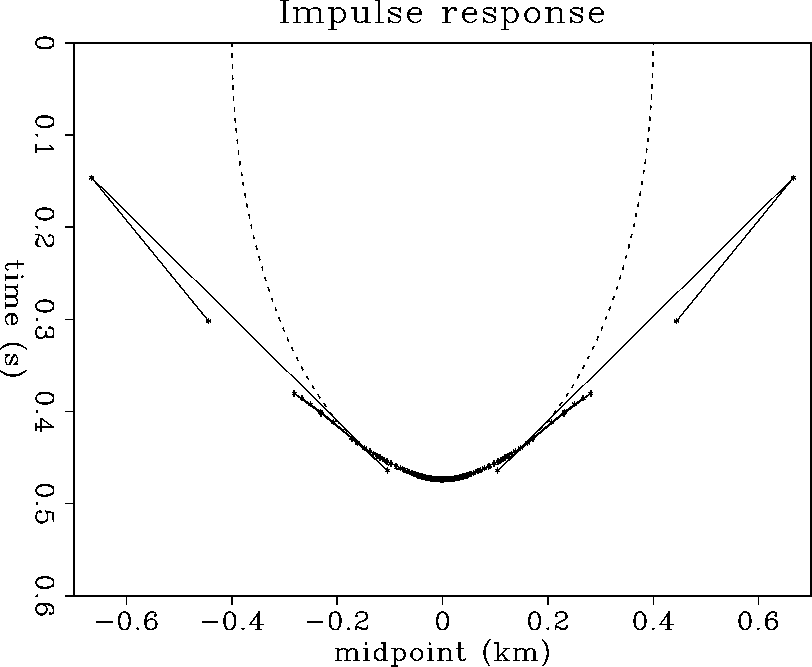 |
Artley's 1992 v(z) dip moveout method
which produced Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , requires a non-linear inversion
of a
, requires a non-linear inversion
of a ![]() system of equations for each time, offset, and dip
we consider. Though it is a time consuming process, it provides us
with amplitude information. First, the triplication of the impulse
response have a low energy for this velocity model (a troff in the
velocity profile would show a high amplitude triplication). Secondly,
the amplitude varies a lot along the operator, starting high at gentle
dips, decreasing, and increasing again just before a triplication.
system of equations for each time, offset, and dip
we consider. Though it is a time consuming process, it provides us
with amplitude information. First, the triplication of the impulse
response have a low energy for this velocity model (a troff in the
velocity profile would show a high amplitude triplication). Secondly,
the amplitude varies a lot along the operator, starting high at gentle
dips, decreasing, and increasing again just before a triplication.
The shape of a v(z) DMO operator differs from the constant-velocity
DMO operator essentially by a number of triplications along its branches
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). However, since these triplications are generally
low-amplitude, the shape is not the most discriminative feature of the
operator. The amplitude variations along the operator strongly depend
on the velocity model, and therefore play the important role in the
dip moveout correction.
). However, since these triplications are generally
low-amplitude, the shape is not the most discriminative feature of the
operator. The amplitude variations along the operator strongly depend
on the velocity model, and therefore play the important role in the
dip moveout correction.