 |
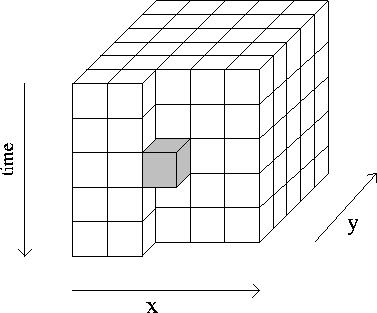
Figure 3 A three-dimensional lateral prediction filter. The darkened cube is the output position.
Extending the t-x prediction to three dimensions is a simple matter of defining the three-dimensional convolution and its adjoint, that is, its conjugate transpose. Instead of dividing the input image into two-dimensional windows, the input volume is broken into three-dimensional subvolumes. Each of these subvolumes is used in a separate least-squares problem for calculating a three-dimensional filter, which is a straightforward extension of the calculation of a two-dimensional t-x filter. Figure 3 shows the configuration of the three-dimensional filter we used. As in the two-dimensional case, the three-dimensional prediction is applied in both forward and reverse spatial directions to maintain the symmetry of the application.
 |