Next: Velocity behavior of Model
Up: HYDRATE FORMATION MODELS
Previous: Hydrate formation only in
The effective dry moduli of the different hydrate frameworks have to be related
to the effective moduli of the same rock-containing fluid. The
effective moduli of a saturated rock can be calculated at seismic
frequencies by means of Gassmann's formulas:
| 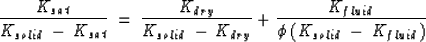 |
(9) |
| 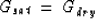 |
(10) |
where Ksat and Gsat are the effective bulk and shear moduli of the
saturated rock; Kdry and Gdry the moduli of the dry rock;
Kfluid and Gfluid the moduli of the fluid; and Ksolid the bulk
modulus of the mineral material making up the rock.
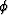 is the porosity of the saturated rock.
is the porosity of the saturated rock.
The effective moduli of the mineral Ksolid can be calculated
using the Voigt-Reuss-Hill average, which is an arithmetic average of
the Voigt upper bound (KV) and the Reuss lower bound (KR):
| 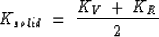 |
(11) |
with
| 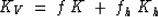 |
(12) |
| 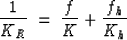 |
(13) |
where f and fh are the volume fractions of the grains and the hydrate,
respectively. K is the grain bulk modulus and Kh is the hydrate
bulk modulus.
In order to calculate the effective fluid bulk modulus Kfluid for
partially-saturated rocks, we used the following equation:
| 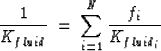 |
(14) |
where fi is the volume fraction of the fluid, N is the number of fluids,
and Kfluid<<188>>i is the bulk modulus of the fluid.
After having derived the effective moduli of the saturated rock, we used the
following relationships to find the seismic velocities in saturated
rock:
| 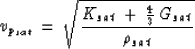 |
(15) |
| 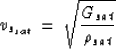 |
(16) |
where 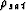 is the density of the saturated rock,
is the density of the saturated rock,
| 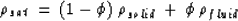 |
(17) |
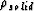 is the density of the solid phase, and
is the density of the solid phase, and 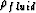 is the
density of the fluid phase which can be obtained from:
is the
density of the fluid phase which can be obtained from:
| 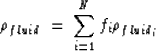 |
(18) |





Next: Velocity behavior of Model
Up: HYDRATE FORMATION MODELS
Previous: Hydrate formation only in
Stanford Exploration Project
11/12/1997
![]() is the porosity of the saturated rock.
is the porosity of the saturated rock.
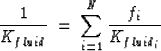
![]() is the density of the saturated rock,
is the density of the saturated rock,