Triangle filters

The idea of the triangle filtering Claerbout (1992a); Lumley et al. (1994) follows from the well-known Nyquist sampling criterion, applied on the stacking-type operator:

 

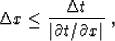$$\Delta x \leq {{\Delta t} \over {\vert\partial t / \partial x\vert}}\;,$$ (6)

where t(x) is the traveltime of the operator imuplse response (or the summation path of the its adjoint). In the steep parts of the traveltime curve, the sampling criterion (6) is not satisfied, which causes aliasing artifacts in the output data. To overcome this problem, the method of triangle filtering suggests convolving the traces of the generated impulse response with a triangle-shaped filter of the length

 

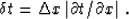$$\delta t = \Delta x\,\vert\partial t / \partial x\vert\;.$$ (7)

Cascading operators of causal and anticausal numerical integration is an efficient way to construct the desired filter shape Bevc and Claerbout (1993).

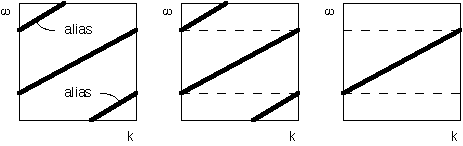
Triangle filters approximate the ideal (sinc) low-pass time filters. The idea behind low-pass filtering as a tool of antialiasing Gray (1992) is illustrated in Figure 4. When a steeply dipping event is included in the operator, its counterpart in the frequency domain wraps around to produce the aliasing artifacts. Those are removed by a dip-dependent low-pass filtering.

 

amolow
Figure 4 Schematic illustration of low-pass antialiasing (triangle filters). The aliased events are removed by low-pass filtration on the temporal frequency axis. The width of the low-pass filter depends on dips of the aliased events.

The method of triangle filtering is less evident in the case of a three-dimensional integral operator. We can take the length of a triangle filter proportional to the absolute value of the time gradient Lumley (1993), the maximum of the gradient components in the two directions of the operator space, or the sum of these components. The latter follows from considering the 3-D operator as a double integration in space. Decoupling the 3-D integral into a cascade of two 2-D operators suggests convolving two triangle filters designed with respect to two coordinates of the operator. In this case, the length of the resultant filter is approximately equal to

 

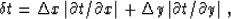$$\delta t = \Delta x\,\vert\partial t / \partial x\vert + \Delta y\,\vert\partial t / \partial y\vert\;,$$ (8)

and its shape is smoother than that of a triangle filter (Figure 5).

 

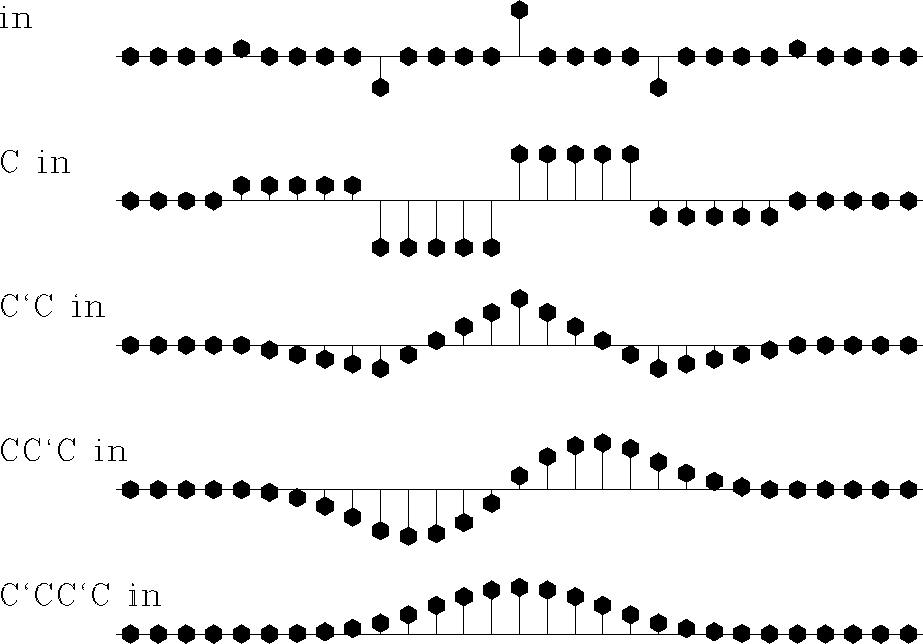
amoflt Figure 5 Building the smoothed filter for 3-D antialiasing by successive integration of a five-point wavelet. C denotes the operator of causal integration, C' denotes its adjoint (the anticausal integration). The result is equivalent to the convolution of two equal triangle filters.

In the case of azimuth moveout, the width of the antialising filter is derived from formula (8) and the travel-time equation (2) as

 

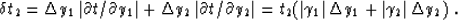$$\delta t_2 = \Delta y_1\,\vert\partial t / \partial y_1\vert... ...t\gamma_1\vert\,\Delta y_1 + \vert\gamma_2\vert\,\Delta y_2)\;.$$ (9)

The triangle filtering method proven an efficient tool in the design of stacking operators of different types. However, we see the following two disadvantages of applying it to the AMO case:

1.

The saddle shape of the AMO operator introduces rapid changes in the length and direction of the traveltime gradient. It leads to an inexact estimation of the triangle length at the curved parts of the operator. Consequently, the high-frequency part of the output can be distorted, causing a loss in the image resolution.

2.

For large input times, most of the energy of the AMO operator is concentrated in the flat part of its traveltime surface (the middle part of the ``saddle''). This part does not contain aliased energy and does not require any sophistication in the time interpolation.