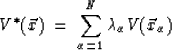
I plan to use GSLIB Deutsch and Journel (1992) to perform both the kriging of the well velocity with the seismic velocity as a trend and the sequential Gaussian simulation (sGs) to calculate a measure of the local and global uncertainties about the estimated model.
The kriging estimated value of the velocity based on the well data and using the seismic velocity model as a linear trend is
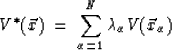 |
(8) |
where coefficients ![]() are estimated by solving
the kriging with a trend (KT) system (9), and
are estimated by solving
the kriging with a trend (KT) system (9), and ![]() are the velocities of the N neighboring points located at position
are the velocities of the N neighboring points located at position
![]() used to determine
used to determine ![]() . The KT system is made of
(N+3) equations:
. The KT system is made of
(N+3) equations:
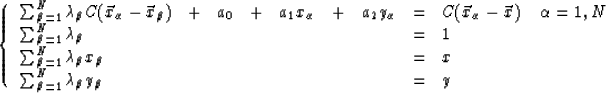 |
(9) |
where ![]() is the covariance of the velocity
at location
is the covariance of the velocity
at location ![]() and location
and location ![]() , and ai are the
coefficients of the linear trend:
, and ai are the
coefficients of the linear trend:
| (10) |
A covariance model
is therefore needed and will be inferred from the semi-variogram ![]() model of the well velocity. By definition,
model of the well velocity. By definition, ![]() is equal to C(0)-C(h).
The sGs will also allow me to estimate a range of equiprobable velocity
models that will require some interpretation in order to produce a measure of
the uncertainty about the estimated velocity model.
is equal to C(0)-C(h).
The sGs will also allow me to estimate a range of equiprobable velocity
models that will require some interpretation in order to produce a measure of
the uncertainty about the estimated velocity model.
The sGs procedure is based on the normal score transform of the velocity random
variable ![]() , assuming that the transformed variable is multi-normal.
When the multi-normality hypothesis cannot be retained, I will use
an indicator simulation instead of the Gaussian approach.
, assuming that the transformed variable is multi-normal.
When the multi-normality hypothesis cannot be retained, I will use
an indicator simulation instead of the Gaussian approach.