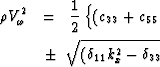 , where the angles
, where the angles
Considering nondispersive media, for the propagation direction ![]() ,
, ![]() , and
, and 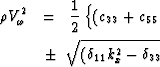 , where the angles
, where the angles
![]() and
and ![]() are measured from the vertical axis and the
medium's symmetry axis, respectively, as shown in Figure 1,
equation (5) produces the following three plane wave modes
(results obtained with the symbolic calculation software package
Mathematica):
are measured from the vertical axis and the
medium's symmetry axis, respectively, as shown in Figure 1,
equation (5) produces the following three plane wave modes
(results obtained with the symbolic calculation software package
Mathematica):
| |
(6) |
 is an arbitrary constant, usually taken as a
normalizing factor.
is an arbitrary constant, usually taken as a
normalizing factor.
This is a pure shear mode, since its direction of particle motion (0,-kz,ky) is always perpendicular to the direction of propagation (kx,ky,kz). This propagation mode is called an SH mode.
The other two solutions are expressed as follows:
| |
||
| (7) | ||
The sign of ``![]() '' selects one of the two remaining modes. The
``+'' sign selects the ``fast'' wave solution, while the ``-''
sign selects the ``slow'' wave solution. For all angles of direction
'' selects one of the two remaining modes. The
``+'' sign selects the ``fast'' wave solution, while the ``-''
sign selects the ``slow'' wave solution. For all angles of direction
![]() and
and ![]() , the fast solution is always greater than the
slow solution. In the case of isotropy, the fast solution corresponds
to the P-wave solution, the slow to the SV-wave. For transverse
isotropy and for anisotropy in general, the fast wave-mode may be
neither a pure P-wave nor an approximate P-wave, just as the slow
wave-mode may be neither a pure SV-wave nor an approximate
SV-wave. For this reason and to avoid bias, it is better to call these
two solutions the fast and the slow wave solutions,
instead of using the conventional notation, qP and qS.
, the fast solution is always greater than the
slow solution. In the case of isotropy, the fast solution corresponds
to the P-wave solution, the slow to the SV-wave. For transverse
isotropy and for anisotropy in general, the fast wave-mode may be
neither a pure P-wave nor an approximate P-wave, just as the slow
wave-mode may be neither a pure SV-wave nor an approximate
SV-wave. For this reason and to avoid bias, it is better to call these
two solutions the fast and the slow wave solutions,
instead of using the conventional notation, qP and qS.
It is important to notice that any plane wave propagating in the y-z plane, will have a constant-value velocity function. This plane is referred to as the isotropy plane (Figure 1).
Even though it may not be obvious from equations (6) and (7), the three propagation modes, fast, slow, and SH, are perpendicular to each other as expected.