




Next: The Fourier version
Up: NOTES FROM TIEMAN's SEMINAR
Previous: The data
Slant stacks are commonly applied to unsorted data, one
shot at a time. This form is well suited to deconvolution
of multiple reflections from flat reflectors. Such multiple
reflections are periodic at zero-offset, but not at a single
finite offset h.
A slant stack attempts to describe our recorded data as
a sum of dipping lines.
A dip ps will measure the slope of
time with offset holding a source position constant.
| 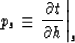 |
(1) |
With ideal sampling and infinite offsets,
this equation would describe a plane-wave
source on the surface. A plane wave reflecting from
flat reflectors would produce periodic multiples at any ps.
Predictive deconvolutions can detect this periodicity and
remove multiple reflections.
The simplest slant-stack sums data over all lines within
a feasible range of dips.
Let 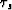 be the intersection at zero offset of our imaginary
plane wave in the shot gather.
be the intersection at zero offset of our imaginary
plane wave in the shot gather.
| 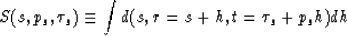 |
(2) |
In practice the integral over offset h must be a discrete
sum with a limited range of offsets.
The inverse of this transform looks much like another slant
stack, with some adjustments of the spectrum. Papers
are readily available to explain this inverse. I will concentrate
instead on the conversion of one type of slant stack to another.





Next: The Fourier version
Up: NOTES FROM TIEMAN's SEMINAR
Previous: The data
Stanford Exploration Project
11/12/1997
![]() be the intersection at zero offset of our imaginary
plane wave in the shot gather.
be the intersection at zero offset of our imaginary
plane wave in the shot gather.