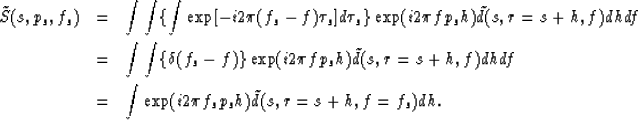Next: The midpoint gather
Up: NOTES FROM TIEMAN's SEMINAR
Previous: A conventional slant stack
Because the time axis is well sampled and unaliased, we can safely
Fourier transform the data between time t and frequency f:
| 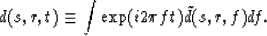 |
(3) |
Tildes will indicate Fourier transforms.
Transform the slant stack from  to its frequency fs:
to its frequency fs:
| 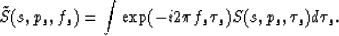 |
(4) |
The slant stack simplifies numerically.
Substitute the transform (3) into the slant stack (2),
then take the transform (4) of both sides of the equation:
| 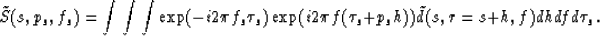 |
(5) |
Rearranging terms, we reduce integrals
| 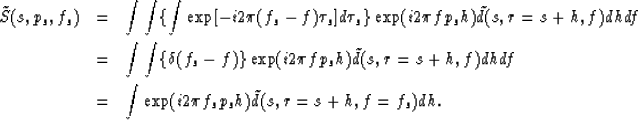 |
|
| |
| (6) |
The second step uses the Fourier transform of a delta function
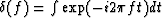 .The third uses
the behavior of a delta function in an integral
.The third uses
the behavior of a delta function in an integral
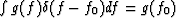 .
.





Next: The midpoint gather
Up: NOTES FROM TIEMAN's SEMINAR
Previous: A conventional slant stack
Stanford Exploration Project
11/12/1997