MEDIANS IN AUTOREGRESSION

Here is an idea for computing autoregression filters. I am not sure what its mathematical properties are, but it seems simpler than other autogression methods and it seems more robust. We load a residual vector with the negative of the data $\bold r=-\bold d$and iterate the following steps:

First take a random direction $\Delta \bold a$.The residual change connected with going this direction is

$$\Delta \bold r \quad =\quad\bold D \; \Delta \bold a$$ (6)

where $\bold D$ is a convolution matrix (matrix of downshifted columns, each containing the data $\bold d$). Now we need to decide an amount $\alpha$ of the perturbation $\Delta \bold a$to be used for our new filter

$$\bold a \longleftarrow \bold a + \alpha \Delta \bold a$$ (7)

We do this by choosing

$$\alpha \quad =\quad-\; \mbox{median}_i\left( { r_i\over \Delta r_i} \right)$$ (8)

This reduces the maximum number of components in $\bold r$.

I experimented with a variety of random and nonrandom directions $\Delta \bold a$.One of my initial guesses $\Delta \bold a = \mbox{sgn}(\bold D') \mbox{sgn}(\bold r)$turned out to be a poor one. Better results were found by cycling, one at a time through each filter component. That saves the cost of the correlation too! I also tried random component values in $\Delta \bold a$.I also tried randomly selecting one component in $\Delta \bold a$to be nonzero. None of these methods would tolerate as much noise as the method in TDF. (In that method, a prior filter (1,-2,1) was guessed, and residuals of it were sorted to point to bursts, which were then weighted by zero.) Some comparisons of the different methods follow:

method   niter     a(1)     a(2)       a(3)     a(4)       a(5)
-----    -----   -------  -------   --------  --------  --------
TDF         10   1.00000  -3.44381   4.91496  -3.44027   0.99767
pefcycle  2000   1.00000  -1.54487   0.77143   0.00011  -0.02502
pefrand   2000   1.00000  -1.65394   0.91726   0.03670  -0.09572
pefrandm  2000   1.00000  -1.72055   0.98708   0.00670  -0.11133

The TDF method is significantly faster as well as being better since instead of requiring infinitely many iterations, it requires only one iteration for each component of $\bold a$.I am disappointed this median method did not work better than the TDF method because the TDF method requires a prior filter and the median method does not.

 

pefdeburst Figure 1 (a) Bichromatic data with bursty noise. (b) Cleaned by L2 method of TDF. (c) Random directions and median distances.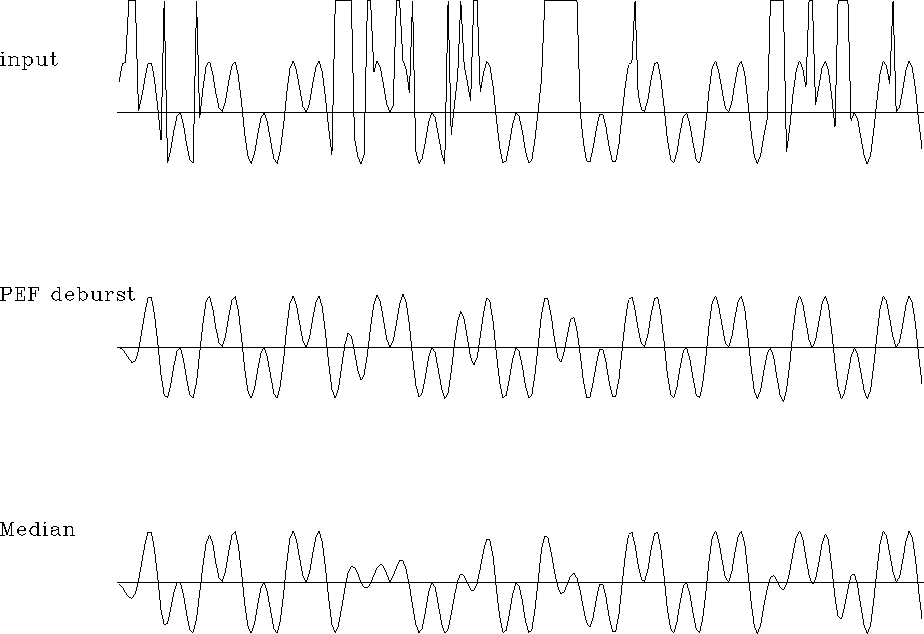

Some comparisons are in Figure 1 which shows, not the autoregressive filters themselves but using the filters, the results of restoration of bad data treating it as missing data. The individual filter coefficients, or random directions, did not work as hoped, but we might have better luck using Levinson's reflection coefficients (not tried).

Let us pursue the idea above that each component of model space can be handled independently, but let us do it in another problem where there are many more components in model space and it seems plausible that many of them would be hardly related. Let us choose a truly huge problem, say inverse hyperbola superposition.