




Next: Geometric interpretation
Up: Schwab et al.: 3-D
Previous: Acknowledgments
- Claerbout, J. F., 1976, Fundamentals of geophysical data processing: Blackwell.
-
- Claerbout, J. F., 1992, Information from smiles: Mono-plane-annihilator weighted regression: SEP-73, 409-420.
-
- Claerbout, J. F., 1993, 3-D local-monoplane annihilator: SEP-77, 19-26.
-
- Claerbout, J. F., 1994, Applications of Three-Dimensional Filtering: Stanford Exploration Project.
-
- Haskell, N. L., Nissen, S. E., Lopez, J. A., and Bahorich, M. S., 1995, 3-D seismic coherency and the imaging of sedimentological features: 65th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1532-1534.
-
- Marfurt, K. J., Scheet, R. M., Sharp, J. A., Cain, G. J., and Harper, M. G., 1995, Suppression of the acquisition footprint for seismic sequence attribute mapping: 65th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 949-952.
-
- Nissen, S. E., Haskell, N. L., Lopez, J. A., Donlon, T. J., and Bahorich, M. S., 1995, 3-D seismic coherency techniques applied to the identification and delineation of slump features: 65th Ann. Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1535-1536.
-
We want to prove that
for a given 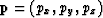 the expression
the expression
| 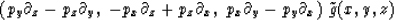 |
(2) |
vanishes for all 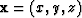 , if and only if
, if and only if
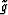 is a volume of parallel planes,
is a volume of parallel planes,
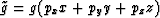 .(
.(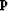 represents the strike of the parallel planes;
g represents a one-dimensional amplitude function).
represents the strike of the parallel planes;
g represents a one-dimensional amplitude function).
First,
we prove that expression (A-1) vanishes for
a volume of parallel, planes.
Applying the chain rule to the first component
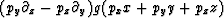 yields
(py g' pz - pz g' py) = 0.
An analogue result
for the two additional components
of expression (A-1)
demonstrates
that the entire expression
vanishes
for a volume
yields
(py g' pz - pz g' py) = 0.
An analogue result
for the two additional components
of expression (A-1)
demonstrates
that the entire expression
vanishes
for a volume 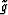 that consists of parallel planes.
that consists of parallel planes.
Next, we prove that if all three components of expression
(A-1) vanish, than the function 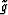 is a
volume of parallel planes.
We set the expression (A-1) to zero and express
it as a vector product of
is a
volume of parallel planes.
We set the expression (A-1) to zero and express
it as a vector product of 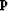 and the gradient of the
field,
and the gradient of the
field, 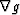 :
:
| 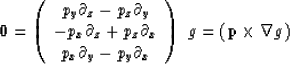 |
(3) |
The vector product of 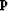 and
and 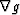 is zero if and
only if one of the vectors is the null vector,
or if the vectors are parallel.
Ignoring the trivial cases, we conclude
that when the outputs of the three finite difference filters vanish
everywhere, than the gradient of g is parallel to the constant
vector
is zero if and
only if one of the vectors is the null vector,
or if the vectors are parallel.
Ignoring the trivial cases, we conclude
that when the outputs of the three finite difference filters vanish
everywhere, than the gradient of g is parallel to the constant
vector 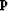 . The constant
. The constant 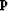 is normal to g at
all locations and
therefore g has to be a volume of parallel planes.
is normal to g at
all locations and
therefore g has to be a volume of parallel planes.





Next: Geometric interpretation
Up: Schwab et al.: 3-D
Previous: Acknowledgments
Stanford Exploration Project
11/12/1997
![]() the expression
the expression
![]() yields
(py g' pz - pz g' py) = 0.
An analogue result
for the two additional components
of expression (A-1)
demonstrates
that the entire expression
vanishes
for a volume
yields
(py g' pz - pz g' py) = 0.
An analogue result
for the two additional components
of expression (A-1)
demonstrates
that the entire expression
vanishes
for a volume ![]() that consists of parallel planes.
that consists of parallel planes.
![]() is a
volume of parallel planes.
We set the expression (A-1) to zero and express
it as a vector product of
is a
volume of parallel planes.
We set the expression (A-1) to zero and express
it as a vector product of ![]() and the gradient of the
field,
and the gradient of the
field, ![]() :
: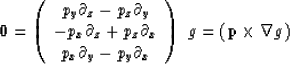
![]() and
and ![]() is zero if and
only if one of the vectors is the null vector,
or if the vectors are parallel.
Ignoring the trivial cases, we conclude
that when the outputs of the three finite difference filters vanish
everywhere, than the gradient of g is parallel to the constant
vector
is zero if and
only if one of the vectors is the null vector,
or if the vectors are parallel.
Ignoring the trivial cases, we conclude
that when the outputs of the three finite difference filters vanish
everywhere, than the gradient of g is parallel to the constant
vector ![]() . The constant
. The constant ![]() is normal to g at
all locations and
therefore g has to be a volume of parallel planes.
is normal to g at
all locations and
therefore g has to be a volume of parallel planes.