Next: FIELD DATA EXAMPLES
Up: Schwab et al.: 3-D
Previous: Rejection of a single
The synthetic subsurface image in Figure 3 simulates a delta with a slump
fault.
The model has horizontal layers near the top,
a Gaussian appearance (the delta sediments) in the middle,
and dipping layers on the bottom.
Horizontal unconformities divide the three regions.
qdmRaw
Figure 3
Synthetic image of a delta with a slump fault.
From left to right:
time-slice from the center of the volume,
North-South section from the edge of the volume,
East-West section from the center of the volume.
The sampling is equal in both spatial directions.
The North-South section runs parallel to the delta's
gradient and therefore seem to be more steeply
dipping than in the center East-West section.
The fault is visible in the time-slice and
the East-West section.





The left image of Figure 3 shows a horizontal
time-slice from the middle of the model.
A careful observer will notice the parabolic fault line in the
center of the plot
(Figure 4 displays the slump fault's location
more visibly and may help locating it in Figure 3).
The image in the center
shows
a vertical slice that corresponds to a cut in the
North-South direction of the original model.
(In general, we use by North-South
and East-West to refer to the map-view
as represented by the time-slice.)
The cut is taken at the western edge of the model.
Consequently, the section follows the gradient of the bedding
and displays the maximal reflector dip of the model.
The right image displays a vertical East-West slice
that cuts the model at its center.
The section intersects the slump fault
The section's apparent bedding
dip is smaller than the dip in the North-South section,
since the center section is not parallel to the bedding's
gradient.
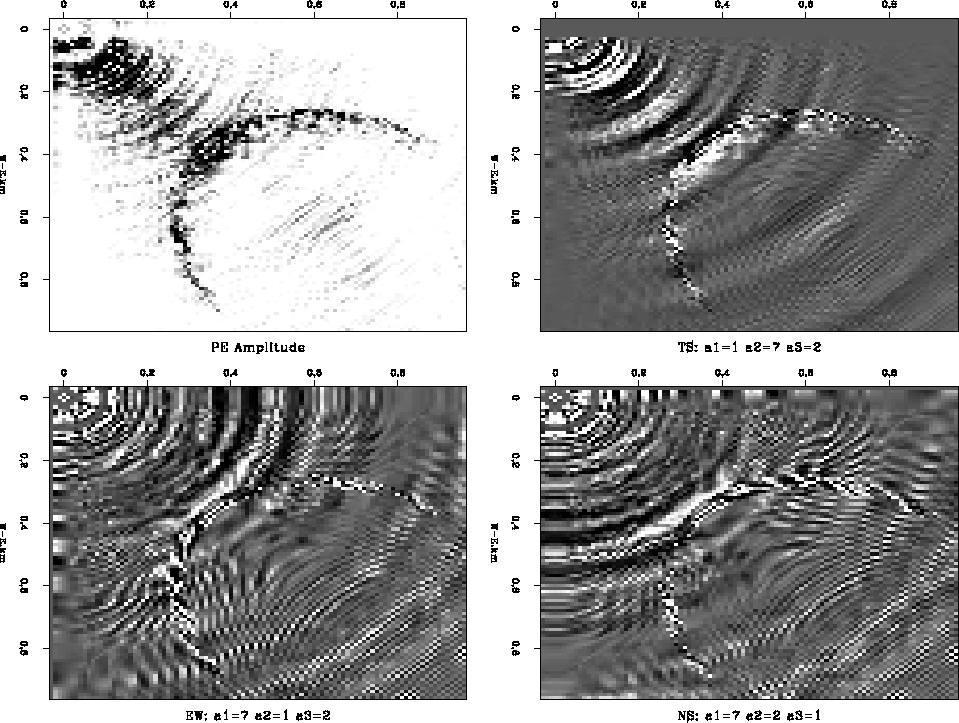
Figure 4 displays the Lomoplan output corresponding
to the time-slice in Figure 3.
The top left plot shows the magnitude of the three Lomoplan output cubes.
The other three plots are the individual Lomoplan residuals.
Each panel is computed
by 2-D prediction error filters operating in a different plane.
The top right plot is generated by 2-D planar PE filters that operate
in the time-slice plane, as the TS of the plot title indicates.
The list a1=1, a2=7, a3=2 of the title expresses the filters'
size: no extension in the depth dimension (thus a
time-slice filter), seven samples in the North-South dimension,
and two samples in the East-West dimension.
The bottom right panel corresponds to vertical PE filters
predicting in the East-West plane. Finally, the bottom left panel
is the output of vertical 2-D PE filters in the North-South
plane.
qdmPef
Figure 4
Lomoplan residuals.
The figures clockwise from the top-left:
Magnitude of the three Lomoplan components
and the three Lomoplan outputs (time-slice, East-West,
North-South).
The time-slice residual has a larger magnitude
than the other sections and consequently
dominates the magnitude plot.





All three Lomoplan residuals in Figure 4 enhance the slump fault.
The slump fault is characterized by relatively strong but random
output values.
All three panels display characteristic noise:
the time-slice prediction could not predict the steeply dipping
and strongly curving events
close to the image's diagonal.
At these locations, the synthetic
model probably violates our assumption that the
model can be locally represented as planar reflector model.
The time-slice filter succeeded, however, in removing the same events
where they were oriented parallel to one of the filter's axes,
as at the northern and western edge of the image.
This may indicate unfavorable directional bias that probably results
from our filter shape.
Both vertical filters display a ringing noise, which might be
related to the interpolation that generated the synthetic image.
The East-West filter perfectly rejects the East-West striking
events at the western edge of the model, but it fails
to reject the steeply North-South dipping events
at the northern edge of the image.
Contrarily, the North-South filter rejects the events
at the northern edge, but fails at the western edge.
This indicates that the filter with depth stepout of seven coefficients
has not sufficed to remove the events of steep apparent dip.
We combined the three Lomoplan outputs by computing
the L-2 norm amplitude of the three component vector residual
(time-slice, East-West, North-South) at each location.
The resulting amplitude at the left top corner of Figure 4
shows no image improvement over the individual residual plots.
The time-slice residual dominates the amplitude plot, since
its values are an order of magnitude larger
than the values of the two vertical residuals.
Since the amplitude plot adds positive numbers, the noise is not
cancelled.
This synthetic model demonstrates our need for a better method
to combine the various residual images of Lomoplan.





Next: FIELD DATA EXAMPLES
Up: Schwab et al.: 3-D
Previous: Rejection of a single
Stanford Exploration Project
11/12/1997