Next: North Sea prestack data
Up: APPLICATION OF WAVELET-BASED COMPRESSION
Previous: Synthetic shot gather
We generate a synthetic 3-D dataset using the formula
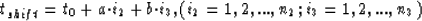
First, a white noise trace is generated and passed through a low-pass filter.
Then, according to the position of the trace on the n2 by n3 plane,
we shift the trace by tshift. As a special case, if we set a=0 and
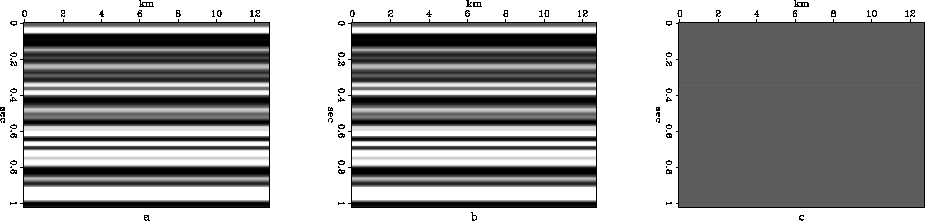
b=0, we will get a dataset consisting of many horizontal reflections,
as shown in Figure 9. Otherwise, we will generate a series of
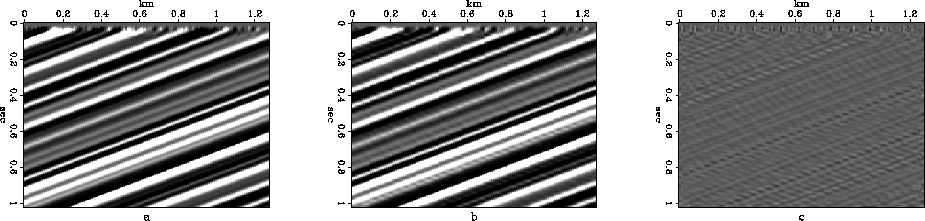
dipping reflections, as shown in Figure 10 (a=1, b=1).
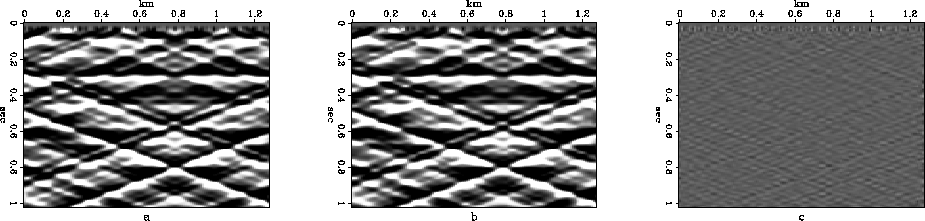
Finally, we mix three datasets of different dipping reflections together
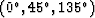 and get a new dataset, as shown in
Figure 11. The size of this cube is n1=256, n2=128, and
n3=128.
and get a new dataset, as shown in
Figure 11. The size of this cube is n1=256, n2=128, and
n3=128.
This dataset mainly consists of coherent component. Therefore, the result from
horizontal reflections is nearly perfect. However, with the increase of
dipping angle, the extent of coherency decreases and the compression
ratio also decreases from several thousand to less than two hundred. This
verifies our analysis in last section, i.e., steep dipping reflections are more
difficult to compress. This is why we prefer to compress the dataset after NMO
correction.
One interesting thing is, the result of the mixing case is better than the
case of 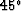 dipping reflections (difference of SNR is 1.17dB).
This is because some high-frequency, high-wavenumber coherent noise is
introduced into the dataset after compression. In the mixing case, the
coherent noise cancels each other. Therefore the influence is not so serious.
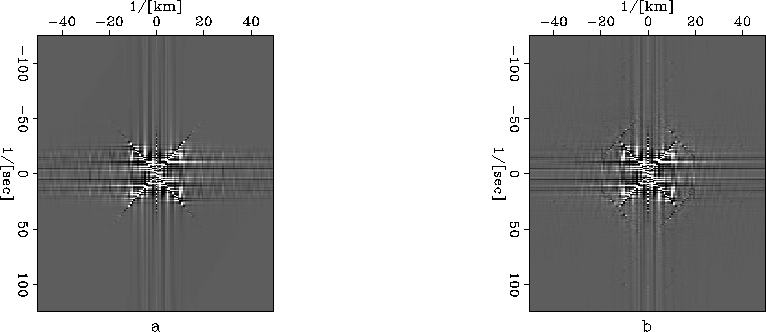
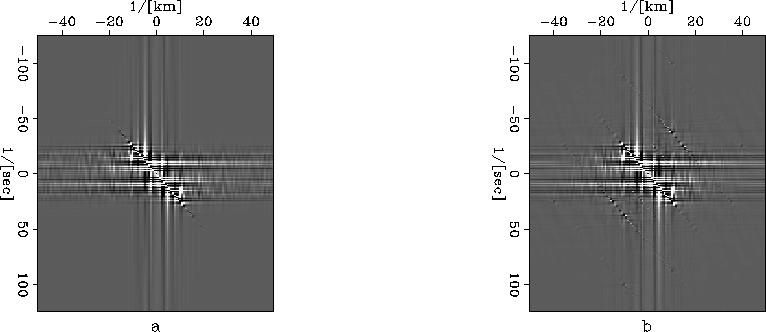
As shown in Figure 12 and 13, it is
very easy to notice the high-frequency, high-wavenumber coherent component in
the f-k domain. In the real seismic dataset, there exist reflections
with many different dipping angles. This coherent noise usually will not
cause big problem.
dipping reflections (difference of SNR is 1.17dB).
This is because some high-frequency, high-wavenumber coherent noise is
introduced into the dataset after compression. In the mixing case, the
coherent noise cancels each other. Therefore the influence is not so serious.
As shown in Figure 12 and 13, it is
very easy to notice the high-frequency, high-wavenumber coherent component in
the f-k domain. In the real seismic dataset, there exist reflections
with many different dipping angles. This coherent noise usually will not
cause big problem.
compdip0
Figure 9 Synthetic horizontal reflection section (scale=0.2). In this case, the compression ratio is 3009 and SNR is 46.91dB.
a: Original dataset.
b: Compressed dataset.
c: Difference of the two datasets.




 compdip45
compdip45
Figure 10 Synthetic dip reflection section (scale=0.28, dipping angle=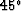 ). In this case, the compression ratio is 149 and SNR is 21.49dB.
). In this case, the compression ratio is 149 and SNR is 21.49dB.
a: Original dataset.
b: Compressed dataset.
c: Difference of the two datasets.




 compdipmix
compdipmix
Figure 11 Mixed section consisting of three different dipping events (scale=0.24, dipping angle=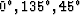 ). In this case, the compression ratio is 151 and SNR is 22.66dB.
). In this case, the compression ratio is 151 and SNR is 22.66dB.
a: Original dataset.
b: Compressed dataset.
c: Difference of the two datasets.




 ftcompdipmix
ftcompdipmix
Figure 12 Mixed section consisting of three different dipping events in f-k domain.
a: Original dataset.
b: Compressed dataset.




 ftcompdip45
ftcompdip45
Figure 13 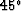 dip reflection section in f-k domain.
dip reflection section in f-k domain.
a: Original dataset.
b: Compressed dataset.










Next: North Sea prestack data
Up: APPLICATION OF WAVELET-BASED COMPRESSION
Previous: Synthetic shot gather
Stanford Exploration Project
11/12/1997
![]()
![]() dipping reflections (difference of SNR is 1.17dB).
This is because some high-frequency, high-wavenumber coherent noise is
introduced into the dataset after compression. In the mixing case, the
coherent noise cancels each other. Therefore the influence is not so serious.
As shown in Figure 12 and 13, it is
very easy to notice the high-frequency, high-wavenumber coherent component in
the f-k domain. In the real seismic dataset, there exist reflections
with many different dipping angles. This coherent noise usually will not
cause big problem.
dipping reflections (difference of SNR is 1.17dB).
This is because some high-frequency, high-wavenumber coherent noise is
introduced into the dataset after compression. In the mixing case, the
coherent noise cancels each other. Therefore the influence is not so serious.
As shown in Figure 12 and 13, it is
very easy to notice the high-frequency, high-wavenumber coherent component in
the f-k domain. In the real seismic dataset, there exist reflections
with many different dipping angles. This coherent noise usually will not
cause big problem.