SYNTHETIC EXPERIMENT

To examine the effects of fold variations on wave equation processes, namely AMO and migration, we tested our normalization technique on the synthetic reflectivity model used by Chemingui and Biondi 1996a to prove their proposed true amplitude sequence for processing wide-azimuth 3D surveys. The model is 10,000 by 10,000 feet wide and simulates a flat reflector with amplitude anomalies along its surface. The anomaly zones take the form of circles of high reflectivity. Figure 4 shows a cross section of the synthetic model taken at the top of the flat reflector. The edges of the model are tapered to avoid numerical diffractions from the modeling algorithm. For the sake of simplicity, we consider a medium with a constant velocity of 10,000 ft/sec. The Button Patch geometry of the survey is discussed in Chemingui and Biondi 1996a. A 3D subset containing 24,000 traces with source-receiver azimuth between -30^o and 30^o and an absolute offset range from 7000 to 9000 ft was extracted from the 5D prestack volume. The nominal CMP spacing is 80 ft in both x and y directions. The new simulations use a high frequency source wavelet to better resolve the details of the reflectivity images. The results are also plotted with high resolution to distinguish the anomalous zones in the constant background.

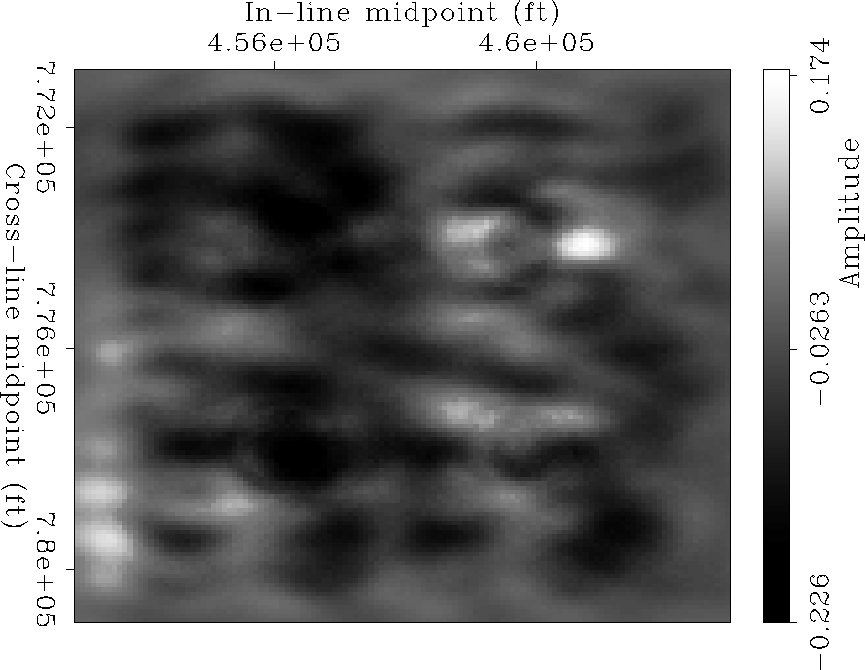
In a first experiment, we migrated the data using a true-amplitude Kirchhoff algorithm without accounting for fold variations. Figure 5 shows the results of the direct migration. The reflectivity map has a poor resolution and suffers amplitude distortions scattered along the entire flat reflector. Figure 6 shows the results of the normalized migration; the image is now smoother, it shows more continuity and better resolution than the unconditioned migration result. The equalization for fold coverage during migration eliminated most of the amplitude distortions along the horizontal reflector and helped image the location of the anomalies.

Next, we applied the AMO transformation to regularize the geometry and reconstruct the data as a zero-azimuth cube with 8000 ft effective offset and constant mid-point spacing of 80 ft. The CA/CO cube is then migrated using the 3D prestack depth migration algorithm. Figures 7 and 8 show the results of this processing sequence. Figure 7 is generated with an AMO algorithm that does not account for the variations in the fold coverage. This is the previous result presented in Chemingui and Biondi (1996b) regenerated and displayed at better resolution. We compare this result to the new image obtained by including the normalization procedure in the integral AMO algorithm. The output of the AMO transformation is a regularly gridded single-fold CA/CO cube well suited for prestack migration. Figure 8 shows that the normalization procedure improved the quality of the reflectivity map and eliminated the foot imprint of the geometry.

The results of the normalized migration and normalized AMO are very similar. The advantage of applying the correction procedure during the AMO transformation is the resulting reduction in the the size of the prestack volume and the regularization of the data into CA/CO cubes for prestack migration. This allows for more reliable amplitude analysis as a function of offset and azimuth.

Figure 9 shows the difference in the reflectivity maps between the unconditioned migration and the normalized migration, whereas Figure 10 shows the difference between the migrated images of the unconditioned AMO and the normalized AMO. The residual maps are very similar and show direct correlation with the fold distribution as displayed on the fold diagram (Figure 3).

 

mig-neq
Figure 5 Reflectivity map obtained by direct Kirchhoff migration without normalization.

 

mig-equ
Figure 6 Reflectivity map obtained by normalized migration.

 

amo-neq
Figure 7 Reflectivity map obtained by migrating the data after applying the AMO transformation to an effective zero-azimuth and a constant offset of 8000 ft without normalization of AMO.

 

amo-equ
Figure 8 Reflectivity map obtained by migrating the data after applying a normalized AMO transformation to zero azimuth and constant offset of 8000 ft.

 

diff-mig
Figure 9 Difference in reflectivity maps between the unconditioned migration and the normalized migration.

 

diff-amo
Figure 10 Difference in migrated images between the unconditioned AMO and the normalized AMO.

We conclude that the normalization of the Kirchhoff operator in its discrete summation implementation helps eliminate the effects of fold variations. It is important to note that this approximate solution for equalization cannot compensate for missing traces or varying spatial distribution of traces within CMP bins. The latter aspect was not a major concern since most redundant traces shared the same spatial coordinates. This is related to the fact that, in land acquisition, Button-Patch geometry in this case, the receiver locations are fixed and geophones are only deployed after the recording of an entire patch.