PYRAMID TRANSFORM

Assume v is medium velocity, $\delta x$ is trace interval and $\theta$ is dip angle, the maximum threshold frequency that is not aliased is as follows Yilmaz (1987):

$$f_{\rm max} = \frac{v}{4\delta x \sin\theta}$$ (1)

We can rewrite the above formula in another form:  

$$\sin\theta = \frac{v}{4f \delta x}$$ (2)

Equation (2) is the relation between the dip angle and the threshold frequency. If f decreases, $\theta$ will increase. Since $0^\circ \le \theta \le 90^\circ$, there is a critical frequency $\bar{f}$ at which  

$$\sin\theta = \frac{v}{4\bar{f}\delta x} = 1$$ (3)

So we conclude that

• For $f<\bar{f}$, the frequency slice contains information up to $90^\circ$. In other words, the data is oversampled.
• For $f\gt\bar{f}$, the frequency slice only contains information $\theta \le \theta_{\rm max} (<90^\circ)$. Dip over $\theta_{\rm max}$ will be aliased. And $\theta_{\rm max}$ is defined by

  $$\theta_{\rm max} = sin^{-1}(\frac{v}{4\bar{f}\delta x})$$

The existence of $\bar{f}$ provides the feasibility of resampling the data in the f-x domain without losing any information. Resampling means that $\delta x$ is no longer constant but a function of frequency, i.e., $\Delta x_{\rm f}$. When $f<\bar{f}$ and $\theta=90^\circ$, equation (2) can be transferred into  

$$\Delta x_{\rm f} = \frac{v}{4f}$$ (4)

Equation (4) shows that we can subsample the frequency slices using larger trace interval. According to sampling theorem, the resampled data does not lose any information theoretically. We call this resampling scheme ``pyramid transform'' and the output a special kind of F-X domain, i.e., pyramid domain.

Figure 1 shows the RHS of equation (3) versus frequency. The solid curve represents the frequency-independent grids. The dash line represents the frequency-dependent grids. From this figure, we can see that all the frequency lower than $\bar{f}=94Hz$ have oversampled the data. Therefore, the next question is what is the disadvantage of oversampling the data?

 

sin-value Figure 1 $\frac{v}{4f\delta x}$ versus f. The solid curve represents the frequency-independent grids. The dash line represents the frequency-dependent grids.

Unless carefully constrained, an over-parameterized model may contain illegal components that will fit noisy data better than a better model which does not include high wavenumbers for low frequencies.

Spatial prediction filters become the same for all frequencies Nichols (1996). Since the prediction filter is independent of frequency, it will become more stable and more insensitive to the noise. Also, we do not need to estimate independent prediction filters for each frequency slice separately.

In any case, oversampling will not bring any profit to noise suppression. So we will use $\delta x$, not $\Delta x_f$, when $f\gt\bar{f}$. Figure 2 shows that when $f\gt\bar{f}$, $\delta x$ is actually the base of another pyramid. So we can regard the input data $(f\gt\bar{f})$ as frequency- dependent grids directly.

In other words, we can get a series of pyramids corresponding to the frequency which is higher than $\bar{f}$. From each pyramid, we can estimate a prediction filter. The difference between the first prediction filter ( $f \le \bar{f}$) and the other ($f\gt\bar{f}$) , is that we can apply the first prediction filter to all the frequencies which are lower than $\bar{f}$. Each of the remaining filters can only be applied to one frequency slice, which is also the base of that pyramid.

 

pyramid
Figure 2 The size of the pyramid(in 2-D, it is actually a triangle) is changing when $(f\gt\bar{f})$.

The basic and most important requirement for pyramid transform is that this transform is invertible. In other words, ``forward'' transform can turn a rectangular f-x domain to a pyramid domain and ``inverse'' transform can turn a pyramid domain back to a rectangular f-x domain, as shown in Figure 3.

 

transform
Figure 3 Schematic demonstration of forward/inverse pyramid transform.

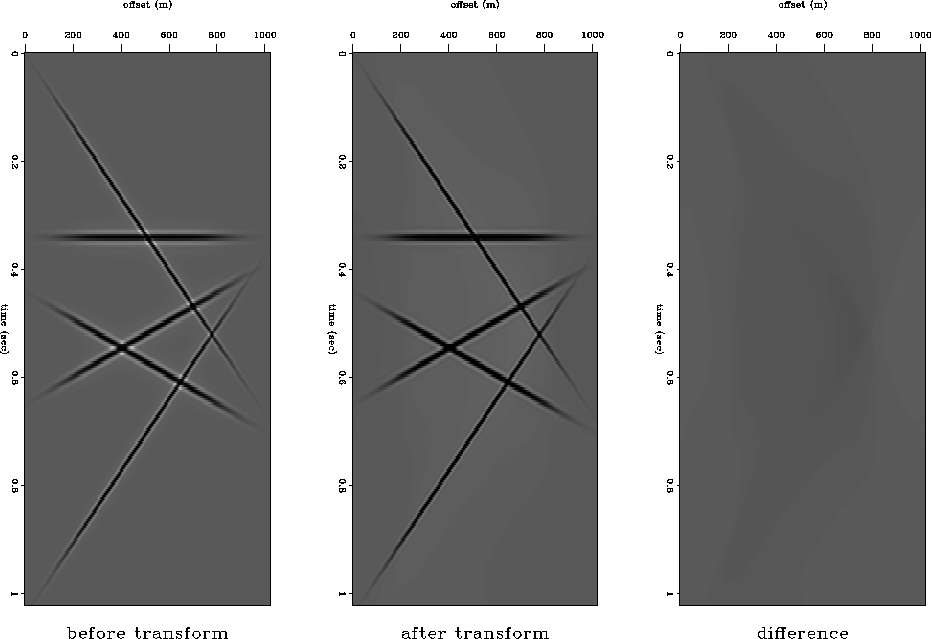
How do we guarantee this transform invertible? The key is to find a good complex-valued interpolation scheme. Here, we use Dave Hale's 8-point sinc interpolation program in SU. Some more accurate and complicated interpolation scheme can be found in Wade's paper 1988. Figure 4 is one example using 8-point sinc interpolation. The result shows that our scheme is very accurate. There is little difference between input and output.

 

forward-inverse-transform
Figure 4 The left is the input dataset, the middle is the result after forward/inverse transform, and the right one is the difference.(Displayed at the same scale)