Next: CONCLUSION AND FUTURE WORK
Up: RESULTS AND DISCUSSION
Previous: Synthetic model (two layers,
This is a synthetic saltdome velocity model issued by EAEG/SEG velocity
modeling committee. The size of the model is 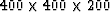 grids and the geometric size of each cube is
grids and the geometric size of each cube is 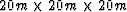 .First, we smooth the model using the same smoothing filter we used
in the last model. Figure 5 shows the portion where the
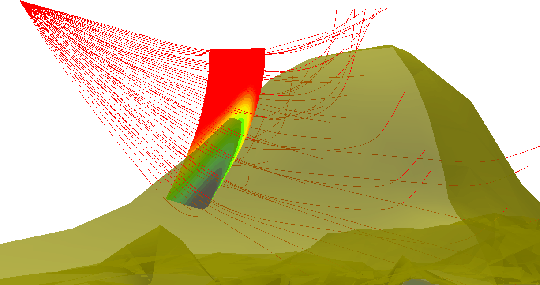
raypaths hit the flank of the saltdome. Since the saltdome velocity is much
higher than the other parts. Most of the rays are ``bounced'' back by the
flank except those rays hitting the flank with small incident angle. We also
show a small portion of the corresponding wavefront. The color of the
wavefront represents the magnitude of the amplitude. The amplitude is
homogeneous before the wavefront hits the saltdome. When the wavefront hits
the flank of saltdome, the amplitude changes quickly because of the wave
resistance.
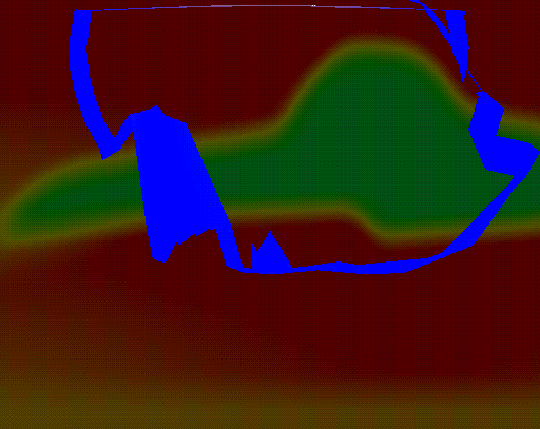
Figure 6 is generated using AVS's clipping function. We use
one model slice and one clipping plane (transparent) to extricate a ring of
wavefront. The model slice shows the saltdome's structure clearly. We can see
several triplications on the ring. This phenomenon is caused by the
complicated velocity model. Therefore it is obvious that first arrival
approach cannot image such a complicated structure. We need to do some
interpolation to get the maximum energy traveltime.
.First, we smooth the model using the same smoothing filter we used
in the last model. Figure 5 shows the portion where the
raypaths hit the flank of the saltdome. Since the saltdome velocity is much
higher than the other parts. Most of the rays are ``bounced'' back by the
flank except those rays hitting the flank with small incident angle. We also
show a small portion of the corresponding wavefront. The color of the
wavefront represents the magnitude of the amplitude. The amplitude is
homogeneous before the wavefront hits the saltdome. When the wavefront hits
the flank of saltdome, the amplitude changes quickly because of the wave
resistance.
Figure 6 is generated using AVS's clipping function. We use
one model slice and one clipping plane (transparent) to extricate a ring of
wavefront. The model slice shows the saltdome's structure clearly. We can see
several triplications on the ring. This phenomenon is caused by the
complicated velocity model. Therefore it is obvious that first arrival
approach cannot image such a complicated structure. We need to do some
interpolation to get the maximum energy traveltime.
model3-ray-front
Figure 5 The raypaths diverge at the flank of saltdome. Variation in amplitude along the wavefront as it enters the
saltdome are also shown, with red;
representing high amplitudes, blue low amplitudes.




 model3-clip
model3-clip
Figure 6 Because of the influence of the saltdome, the wavefront becomes complicated.










Next: CONCLUSION AND FUTURE WORK
Up: RESULTS AND DISCUSSION
Previous: Synthetic model (two layers,
Stanford Exploration Project
11/11/1997
![]() grids and the geometric size of each cube is
grids and the geometric size of each cube is ![]() .First, we smooth the model using the same smoothing filter we used
in the last model. Figure 5 shows the portion where the
raypaths hit the flank of the saltdome. Since the saltdome velocity is much
higher than the other parts. Most of the rays are ``bounced'' back by the
flank except those rays hitting the flank with small incident angle. We also
show a small portion of the corresponding wavefront. The color of the
wavefront represents the magnitude of the amplitude. The amplitude is
homogeneous before the wavefront hits the saltdome. When the wavefront hits
the flank of saltdome, the amplitude changes quickly because of the wave
resistance.
Figure 6 is generated using AVS's clipping function. We use
one model slice and one clipping plane (transparent) to extricate a ring of
wavefront. The model slice shows the saltdome's structure clearly. We can see
several triplications on the ring. This phenomenon is caused by the
complicated velocity model. Therefore it is obvious that first arrival
approach cannot image such a complicated structure. We need to do some
interpolation to get the maximum energy traveltime.
.First, we smooth the model using the same smoothing filter we used
in the last model. Figure 5 shows the portion where the
raypaths hit the flank of the saltdome. Since the saltdome velocity is much
higher than the other parts. Most of the rays are ``bounced'' back by the
flank except those rays hitting the flank with small incident angle. We also
show a small portion of the corresponding wavefront. The color of the
wavefront represents the magnitude of the amplitude. The amplitude is
homogeneous before the wavefront hits the saltdome. When the wavefront hits
the flank of saltdome, the amplitude changes quickly because of the wave
resistance.
Figure 6 is generated using AVS's clipping function. We use
one model slice and one clipping plane (transparent) to extricate a ring of
wavefront. The model slice shows the saltdome's structure clearly. We can see
several triplications on the ring. This phenomenon is caused by the
complicated velocity model. Therefore it is obvious that first arrival
approach cannot image such a complicated structure. We need to do some
interpolation to get the maximum energy traveltime.