EXAMPLES OF SIMPLE 2-D RECURSIVE FILTERS

Figures 3 and 4 contain this 2-D filter  

$$\left[ \begin{array} {cc} 0 & -1/4 \\ 1 & -1/4 \\ -1/4 & -1/4 \end{array} \right]$$ (3)

Let us experiment using this 2-D filter as a recursive filter. In Figure 3 the input is shown on the left. This input contains the filter (3) near the top of the frame and some impulses near the bottom boundary. The second frame in Figure 3 is the result of deconvolution by the filter (3). Notice that deconvolution turns the filter itself into an impulse, while it turns the impulses into comet-like images. The use of a helix is evident by the comet images wrapping around the vertical axis.

 

wrap
Figure 3 Illustration of 2-D deconvolution. Left is the input. Right is after deconvolution with the filter (3)

In Figure 4, many inputs are tested. Starting from the left are a low-pass blob, a Ricker wavelet, the filter (3) itself, and a couple impulses, one near the bottom boundary. The second frame shows deconvolution by the filter (3). The third frame compounds the second frame with an adjoint (reverse time) deconvolution. (Instead of blowing plumes to the right, it blows them to the left.) The fourth frame convolves the result with the original filter and its adjoint; and we see we are back where we started. No errors, no evidence remains of any of the boundaries where we have wrapped and truncated!

 

pdadj
Figure 4 Recursive filtering backwards (leftward on the space axis) is done by the adjoint of 2-D deconvolution. Here we see that 2-D deconvolution compounded with its adjoint is exactly inverted by 2-D convolution and its adjoint.

I found myself with a powerful convolution/deconvolution program, but I did not have a bag full of 2-D filters. Further, I knew that a great number of filters are unstable for deconvolution. I recalled an ancient 1-D theorem that if the sum of the absolute values of the filter coefficients after the onset pulse is less than the pulse, then the filter is ``positive real,'' hence ``minimum phase,'' hence stable in polynomial division. Ironically, it is the ``almost unstable'' filters that hold the greatest interest, because they are the ones that move energy long distances. To make long impulse-responses of deconvolution, I chose all the adjustable filter coefficients to be negative and to sum to -1, as does (3). For damping, I took the absolute value of the sum to be a little less than 1.

In seismology we often have occasion to steer summation along beams. Such an impulse response is shown in Figure 5.

 

dip
Figure 5 This filter is my guess at a simple low-order 2-D filter whose inverse times its inverse adjoint, is approximately a dipping seismic arrival.

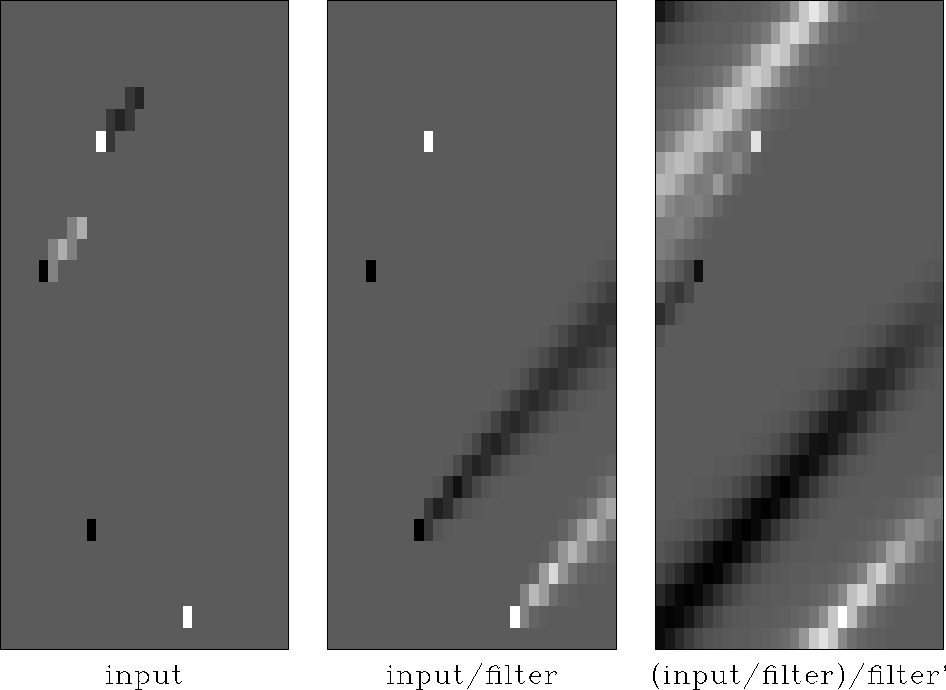Finally, I have long had an interest in filters that would destroy plane waves. The inverse of such a filter creates plane waves. A filter that creates two plane waves is illustrated in figure 6.

 

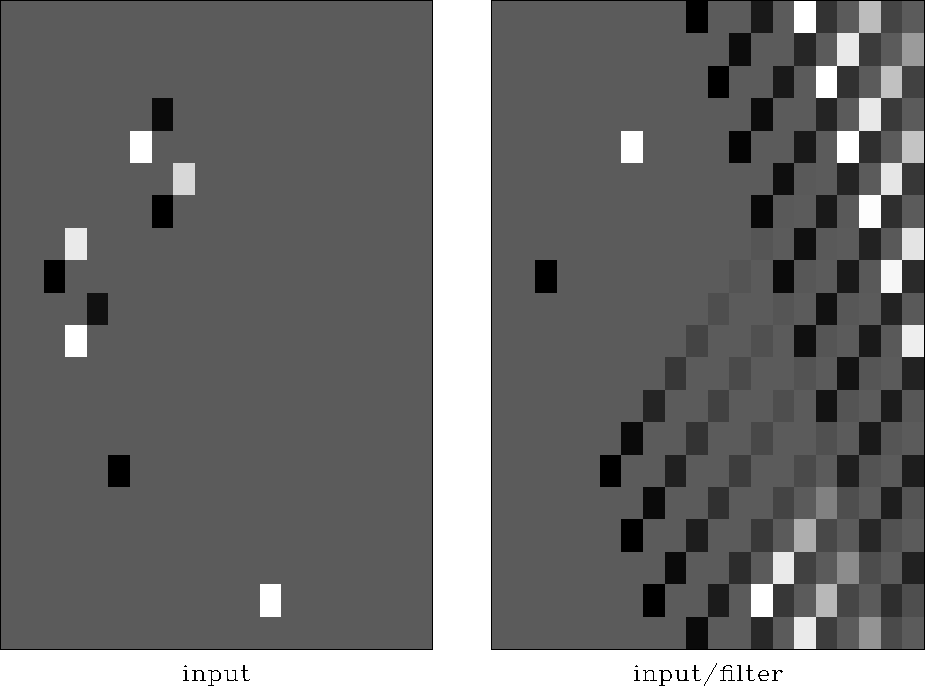waves
Figure 6 This filter is my guess at a simple low-order 2-D filter whose inverse contains plane waves of two different dips. One of them is spatially aliased.