Data-space preconditioning

This is equivalent to pre-multiplying L by the diagonal matrix 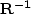${\bf R^{-1}}$and solving the system:

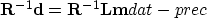$$\bold R^{-1} \bold d = \bold R^{-1} \bold L \bold m \EQNLABEL{dat-prec}$$ (14)

The data-space preconditioner can be interpreted as an approximation to a ``data covariance'' operator that is used to express the reliability and the correlation of the data measurements. In iteratively re-weighted least squares, it approximates a data variance measure that can be estimated from the current residual Nichols (1994).