




Next: SYNTHETIC EXAMPLE
Up: Inversion to common offset
Previous: Data-space preconditioning
The technique is based on a post-multiplication of the matrix
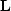 by the diagonal matrix
by the diagonal matrix 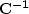 .
.
The preconditioning operator introduces a new model  given by
given by
| 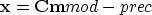 |
(15) |
By the preconditioning transformation, we have recast the
original inversion relation equ1 into
| 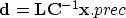 |
(16) |
After solving for  we easily compute
we easily compute
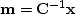 .
.





Next: SYNTHETIC EXAMPLE
Up: Inversion to common offset
Previous: Data-space preconditioning
Stanford Exploration Project
7/5/1998
![]() by the diagonal matrix
by the diagonal matrix ![]() .
.![]() given by
given by
![]() we easily compute
we easily compute
![]() .
.