Azimuth moveout correction in homogeneous media

The impulse response of the AMO operator in homegeneous media is a skewed saddle. The shape of the saddle depends on the offset vector of the input data ${\bf h}_{1}=h_{1}\cos\theta_{1}{\bf x}+h_{1}\sin\theta_{1}{\bf y}=h_{1}(\cos\theta_{1},\sin\theta_{1})$and on the offset vector of the desired output data ${\bf h}_{2}=h_{2} (\cos \theta_{2},\sin \theta_{2})$, where the unit vectors $\bf x$ and $\bf y$ point respectively in the in-line direction and the cross-line direction. The time shift to be applied to the data is a function of the difference vector ${\bf \Delta m}=\Delta m(\cos \Delta \varphi,\sin \Delta \varphi)$ between the midpoint of the input trace and the midpoint of the output trace. The analytical expression of the AMO saddle, is  

$${t}_{2}\left({{\bf \Delta m}},{{\bf h}_{1}},{{\bf h}_{2}},{t... ...\theta_1-\theta_2)-\Delta m^2\sin^2(\theta_1-\Delta \varphi)}}.$$ (1)

The traveltimes t₁ and t₂ are respectively the traveltime of the input data after NMO has been applied, and the traveltime of the results before inverse NMO has been applied.

Figure 2 shows three AMO operators that correspond to three different azimuth correction angles in a homogeneous medium. From left to right, the azimuth corrections are 15, 30, and 45 degrees, respectively. The input and output offset were the same and equal to 2 km. Though the general shape of the AMO operator is practically the same between the three operators, the size is very much dependent on the amount of azimuth correction; the larger the azimuth correction the larger the AMO operator. Clearly, for zero azimuth correction the operator reduces to a point. The size dependence of the operator on azimuth holds regardless of the medium. The shape of the operator, however, is very much independent of azimuth correction.

 

Amo-homo3
Figure 2 AMO operators for isotropic homogeneous media for an input and output offset of 2 km and correction to only the azimuth. The azimuth corrections from left plot to right are 15, 30, and 45 degrees, respectively. The velocity of the homogeneous isotropic medium is 2 km/s, and the input NMO corrected time is 2 s. The x₀ (inline) and y₀ (crossline) axis are in km and the t₀ is in seconds. This holds here and throughout. The circular lines are contours of equal ray parameter.

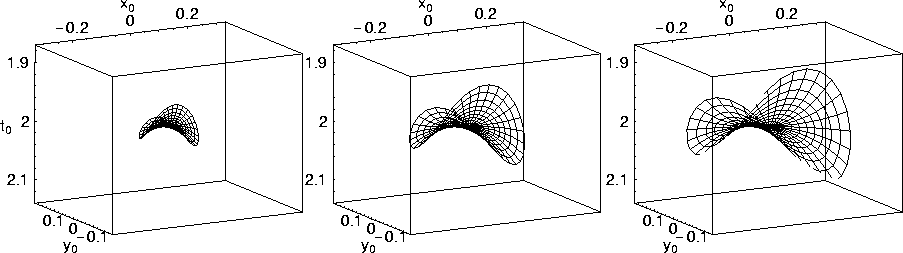In Figure 2 and throughout, the contour curves plotted represent lines of equal ray parameter. It provides information on the distribution of dip angles, as well as on the distribution of energy along the operator; denser contour lines imply higher amplitude.