Next: FIRST RESULTS
Up: Fomel & Claerbout: Galilee
Previous: Introduction
The theory of inverse linear interpolation with a known filter is
given in Applications of Three-Dimensional Filtering
Claerbout (1994), section 2.6, and can be easily extended to
the 2-D case. The algorithm is based on the following procedure. To invert
the data vector 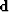 given on an irregular grid for a regularly sampled
model
given on an irregular grid for a regularly sampled
model 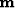 ,
we run the conjugate-gradient solver on the system of equations
,
we run the conjugate-gradient solver on the system of equations
| 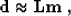 |
(1) |
| 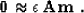 |
(2) |
Equation (1) formulates the basic assumption of the method,
stating that the data
is related to
the model with a linear interpolation operator 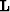 . The next equation
(2) is required to
constrain an underdetermined part of the inverse problem. Minimizing the
output power
of the model
filtered by some roughening filter
. The next equation
(2) is required to
constrain an underdetermined part of the inverse problem. Minimizing the
output power
of the model
filtered by some roughening filter 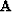 is a way to smooth the
model components that are not determined by equation (1).
Laplacian filter of
the form
is a way to smooth the
model components that are not determined by equation (1).
Laplacian filter of
the form
| 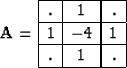 |
(3) |
is a conventional choice for smoothing in two dimensions.





Next: FIRST RESULTS
Up: Fomel & Claerbout: Galilee
Previous: Introduction
Stanford Exploration Project
9/11/2000
![]() given on an irregular grid for a regularly sampled
model
given on an irregular grid for a regularly sampled
model ![]() ,
we run the conjugate-gradient solver on the system of equations
,
we run the conjugate-gradient solver on the system of equations