Next: NARROW-BAND FILTERS
Up: One-sided functions
Previous: FILTERS IN PARALLEL
Two similar types of functions
called admittance functions Y(Z) and
impedance functions I(Z) occur in many physical problems.
In electronics, they are ratios of
current to voltage and of voltage to current;
in acoustics, impedance is the ratio of pressure to velocity.
When the appropriate electrical network or acoustical region
contains no sources of energy, then these ratios have
the positive real property. To see this in a mechanical example,
we may imagine applying a known force F(Z) and
observing the resulting velocity V(Z).
In filter theory, it is like considering that F(Z) is input
to a filter Y(Z) giving output V(Z). We have
|  |
(14) |
The filter Y(Z) is obviously causal.
Since we believe we can do it the other way around,
that is, prescribe the velocity and observe the force,
there must exist a convergent causal I(Z) such that
|  |
(15) |
Since Y and I are inverses of one another
and since they are both presumed bounded and causal,
then they both must be minimum phase.
First, before we consider any physics,
note that if the complex number a + ib
has a positive real part a,
then the real part of (a + ib)-1 namely a/(a2 + b2)
is also positive. Taking a + ib to represent a value of
Y(Z) or I(Z) on the unit circle, we see the obvious fact
that if either Y or I has the positive real property,
then the other does, too.
Power dissipated is the product of force times velocity, that is
| 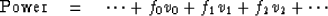 |
(16) |
This may be expressed in terms of Z transforms as
| ![\begin{eqnarray}
\mbox{Power}
&= & {1\over 2}\; \mbox{coeff of}\; Z^0 \: \mbox{...
... Z\right) F(Z) \, + F\left(1\over Z\right)V(Z)\right]
\, d\omega\end{eqnarray}](img40.gif) |
|
| (17) |
Using (14) to eliminate V(Z) we get
| ![\begin{displaymath}
\mbox{Power} \eq {1 \over 2} \, {1 \over 2\pi} \int^{+\pi}_{...
...) \left[Y\left(1 \over Z\right) + Y(Z)\right]
F(Z) \, d\omega \end{displaymath}](img41.gif) |
(18) |
We note that Y(Z) + Y(1/Z) looks superficially like a
spectrum because the coefficient of Zk equals that of Z-k,
which shows the symmetry of an autocorrelation function. Defining
| 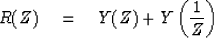 |
(19) |
(17) becomes
| 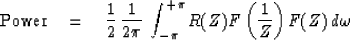 |
(20) |
The integrand is the product of the arbitrary positive
input force spectrum and R(Z). If the power dissipation
is expected to be positive at all frequencies (for all 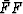 ),
then obviously R(Z) must be positive at all frequencies;
thus R is indeed a spectrum. Since we have now discovered
that Y(Z) and Y(1/Z) must be positive for all frequencies,
we have discovered that Y(Z) is not an arbitrary
minimum-phase filter. The real part of both
Y(Z) and Y(1/Z) is
),
then obviously R(Z) must be positive at all frequencies;
thus R is indeed a spectrum. Since we have now discovered
that Y(Z) and Y(1/Z) must be positive for all frequencies,
we have discovered that Y(Z) is not an arbitrary
minimum-phase filter. The real part of both
Y(Z) and Y(1/Z) is
| ![\begin{displaymath}
\mbox{Re}[Y(Z)] \eq \mbox{Re} \left[ Y\left( 1 \over Z\right...
..., y_o + y_1 \;\cos \; \omega + y_2 \; \cos \; 2\omega + \cdots \end{displaymath}](img45.gif) |
(21) |
Since the real part of the sum must be positive,
then obviously the real part of each of the equal parts
be positive.
Now if the material or mechanism being studied is passive
(contains no energy sources) then we must have positive
dissipation over a time gate from minus infinity up to
any time t. Let us find an expression for dissipation
in such a time gate. For simplicity take both the force
and velocity vanishing before t = 0. Let the end of
the time gate include the point t = 2 but not t = 3.
Define
| 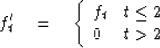 |
(22) |
To find the work done over all time we may integrate (20)
over all frequencies. To find the work done in the selected
gate we may replace F by F' and integrate over all
frequencies, namely
| 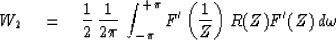 |
(23) |
As we have seen, this integral merely selects
the coefficient of Z0 of the integrand. Let us work
this out. First, collect coefficients of powers of Z
in R(Z)F'(Z). We have
To obtain the coefficient of Z0 in
F'(1/Z)[R(Z)F'(Z)] we must multiply the top row
above by f'0, the second row by f'1 and
the third row by f'2. The result can be arranged
in a very orderly fashion by
| ![\begin{eqnarray}
W_2 &= & {1 \over 2} [f_0 \; f_1 \; f_2]
\left[
\begin{array}
...
...
\left[
\begin{array}
{l}
f_0 \\ f_1 \\ f_2 \end{array} \right]\end{eqnarray}](img49.gif) |
|
| (24) |
Not only must the 3 x 3 quadratic form (24)
be positive (i.e., 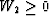 for arbitrary ft) but all
for arbitrary ft) but all
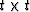 similar quadratic forms Wt must be positive.
similar quadratic forms Wt must be positive.
In conclusion, the positive real property in the frequency
domain means that Y(Z) + Y(1/Z) is positive for any real
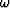 and the positive real property in the time domain
means that all
and the positive real property in the time domain
means that all 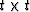 matrices like that of (24)
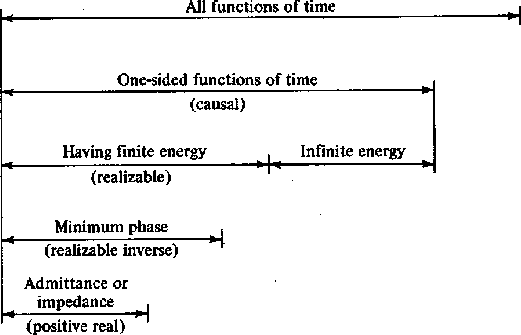
are positive definite. Figure 12 summarizes
the function types which we have considered.
matrices like that of (24)
are positive definite. Figure 12 summarizes
the function types which we have considered.
2-12
Figure 12
Important classes of time functions.

EXERCISES:
- In mechanics we have force and velocity of a
free unit mass related by dv/dt = f or
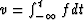 .
Compute the power dissipated as a function of frequency if
integration is approximated by convolution with
(.5, 1., 1., 1., ...). [HINT:
Expand (1 + Z)/ 2(1 - Z) in positive powers of Z.]
.
Compute the power dissipated as a function of frequency if
integration is approximated by convolution with
(.5, 1., 1., 1., ...). [HINT:
Expand (1 + Z)/ 2(1 - Z) in positive powers of Z.]
- Construct an example of a simple function
which is minimum phase but not positive real.





Next: NARROW-BAND FILTERS
Up: One-sided functions
Previous: FILTERS IN PARALLEL
Stanford Exploration Project
10/30/1997
![\begin{eqnarray}
\mbox{Power}
&= & {1\over 2}\; \mbox{coeff of}\; Z^0 \: \mbox{...
... Z\right) F(Z) \, + F\left(1\over Z\right)V(Z)\right]
\, d\omega\end{eqnarray}](img40.gif)
![]() ),
then obviously R(Z) must be positive at all frequencies;
thus R is indeed a spectrum. Since we have now discovered
that Y(Z) and Y(1/Z) must be positive for all frequencies,
we have discovered that Y(Z) is not an arbitrary
minimum-phase filter. The real part of both
Y(Z) and Y(1/Z) is
),
then obviously R(Z) must be positive at all frequencies;
thus R is indeed a spectrum. Since we have now discovered
that Y(Z) and Y(1/Z) must be positive for all frequencies,
we have discovered that Y(Z) is not an arbitrary
minimum-phase filter. The real part of both
Y(Z) and Y(1/Z) is
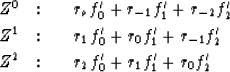
![\begin{eqnarray}
W_2 &= & {1 \over 2} [f_0 \; f_1 \; f_2]
\left[
\begin{array}
...
...
\left[
\begin{array}
{l}
f_0 \\ f_1 \\ f_2 \end{array} \right]\end{eqnarray}](img49.gif)
![]() and the positive real property in the time domain
means that all
and the positive real property in the time domain
means that all ![]() matrices like that of (24)
are positive definite. Figure 12 summarizes
the function types which we have considered.
matrices like that of (24)
are positive definite. Figure 12 summarizes
the function types which we have considered.