ALL-PASS FILTERS

In this section we consider filters with constant unit spectra, that is, $B(Z) \bar {B}(1/Z) = 1$.In other words, in the frequency domain B(Z) takes the form $e^{i \phi (\omega)}$ where $\phi$ is real and is called the phase shift. Clearly $B \bar{B} = 1$ for all real $\phi$.It is an easy matter to construct a filter with any desired phase shift; one merely Fourier transforms $e^{i \phi (\omega)}$ into the time domain. If $\phi(\omega)$ is arbitrary, the resulting time function is likely to be two-sided. Since we are interested in physical processes which are causal, we may wonder what class of functions $\phi(\omega)$ corresponds to one-sided time functions. The easiest way to proceed is to begin with a simple case of a single-pole, single-zero all-pass filter. Then more elaborate all-pass filters can be made up by cascading these simple filters. Consider the filter

 

$$P(Z) \eq {Z - 1/ (\bar{Z})_0 \over 1 - Z/Z_0}$$ (35)

Note that this is a simple case of functions of the form $Z^N \bar{A}(1/Z)/A(Z)$, where A(Z) is a polynomial of degree N or less. Now observe that the spectrum of the filter p_t is indeed a frequency-independent constant. The spectrum is

 

$$\bar {P} \left( 1 \over Z\right) P(Z) \eq {1/Z - 1/Z_0 \over 1 - 1/(Z \bar{Z}_0)} {Z - 1/ \bar{Z}_0 \over Z - 1/Z_0}$$ (36)

Multiply top and bottom on the left by Z. We now have

 

$$\bar {P} \left( 1 \over Z\right) P(Z) \eq {1 - Z/Z_0 \over Z - 1/ \bar {Z}_0} {Z - 1/ \bar {Z}_0 \over 1 - Z/Z_0} \eq 1$$ (37)

It is easy to show that $\bar{P}(1/Z)P(Z) = 1$ for the general form $P(Z) = Z^N \bar{A}(1/Z)/A(Z)$.If Z₀ is chosen outside the unit circle, then the denominator of (35) can be expanded in positive powers of Z and the expansion in convergent on the unit circle. This means that causality is equivalent to Z₀ outside the unit circle. Setting the numerator of P(Z) equal to zero, we discover that the zero $Z = 1/ \bar{Z}_0$ is then inside the unit circle. The situation is depicted in Figure 17. To see that the pole and zero are on the same radius line, express Z₀ in polar form $r_0 e^{i\phi_0}$.

 

2-17 Figure 17 The pole of the all-phase filter lies outside the unit circle and the zero is inside. They lie on the same radius line.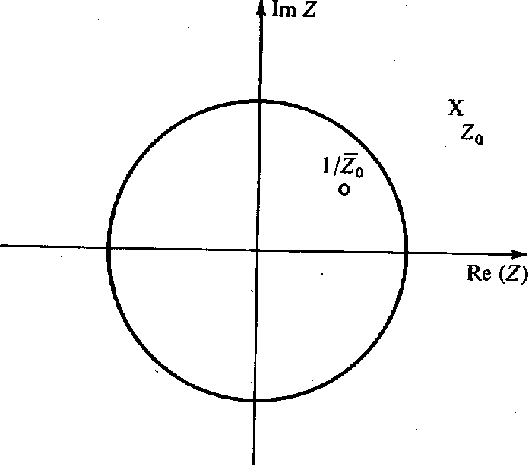

From Section 2.2 (on minimum phase) we see that the numerator of P is not minimum phase and its phase is augmented by $2\pi$ as $\omega$goes from 0 to $2\pi$.Thus the average delay $d \phi / d \omega$ is positive. Not only is the average positive but, in fact, the group delay turns out to be positive in every frequency. To see this, first note that

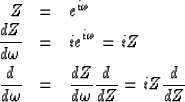$$\begin{eqnarray} Z &= & e^{i\omega} \nonumber \\ {dZ \over d\omega} &= & ie^{... ...r d\omega} &= & {dZ \over d\omega} {d \over dZ} = iZ {d \over dZ}\end{eqnarray}$$ (38)

The phase of the all-pass filter (or any complex number) may be written as  

$$\phi \eq \ln \, P(Z)$$ (39)

Since $\vert P \vert = 1$the real part of the log vanishes; and so, for the all-pass filter (only) we may specialize (39) to

$$\begin{eqnarray} \phi &= & {1 \over i} \ln P(Z) \eq {1 \over i} \ln {Z -1/ \ba... ...ver Z_0} \right) - \ln \left ( 1 - {Z \over Z_0} \right) \right ]\end{eqnarray}$$ (40)

Using (38) the group delay is now found to be

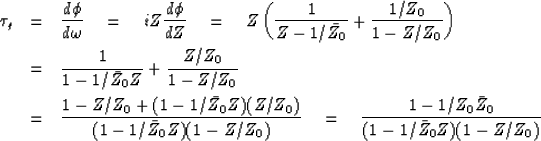$$\begin{eqnarray} \tau_g &= & {d\phi \over d\omega} \eq iZ {d \phi \over dZ} \e... ... \eq {1 - 1/Z_0 \bar{Z}_0 \over (1 - 1/ \bar{Z}_0 Z)(1 - Z/Z_0)}\end{eqnarray}$$ (41)

The numerator of (41) is a positive real number (since $\vert Z_0 \vert \gt 1$), and the denominator is of the form $\bar{A}(1/Z)A(Z)$, which is a spectrum and also positive. Thus we have shown that the group delay of this causal all-pass filter is always positive.

Now if we take a filter and follow it will an all-pass filter, the phases add and the group delay of the composite filter must necessarily be greater than the group delay of original filter. By the same reasoning the minimum-phase filter must have less group delay than any other filter with the same spectrum.

In summary, a single-pole, single-zero all-pass filter passes all frequency components with constant gain and a phase shift which may be adjusted by the placement of a pole. Taking Z₀ near the unit circle causes most of the phase shift to be concentrated near the frequency where the pole is located. Taking the pole further away causes the delay to be spread over more frequencies. Complicated phase shifts or group delays may be built up by cascading several single-pole filters.

EXERCISES:

1. An example of an all-pass filter is the time function $p_t = ({1\over 2}, -{3\over 4}, -{3\over 8}, -{3\over 16}, \cdots)$. Calculate a few lags of its autocorrelation by summing some infinite series.
2. Sketch the amplitude, phase, and group delay of the all-pass filter $(1 - \bar{Z}_0 Z)/(Z_0 - Z)$where $Z_0 = (1 + \varepsilon)e^{i \omega_0}$ and $\varepsilon$ is small. Indicate important parameters on the curve.
3. Show that the coefficients of an all-pass, phase-shifting filter made by cascading $(1 - \bar{Z}_0 Z)/(Z_0 - Z)$ with $(1 - Z_0 Z)/(\bar{Z}_0 - Z)$ are real.
4. A continuous time function is the impulse response of a continuous-time, all-pass filter. Describe the function in both time domain and frequency domain. Interchange the words time and frequency in your description of the function. What is a physical example of such a function? What happens to the statement: ``The group delay of an all-pass filter is positive."?
5. A graph of the group delay $\tau_g (\omega)$in equation (41) shows $\tau_g$ to be positive for all $\omega$. What is the area under $\tau_g$ in the range $0 < \omega < 2\pi$.(HINT: This is a trick question you can solve in your head.)