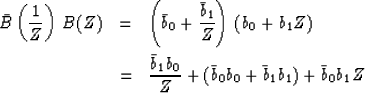
The time function (2, 1) has the same spectrum as the time function (1, 2). The autocorrelation is (2, 5, 2). We may utilize this observation to explore the multiplicity of all time functions with the same autocorrelation and spectrum. It would seem that the time reverse of any function would have the same autocorrelation as the function. Actually, certain applications will involve complex time series; therefore we should make the more precise statement that any wavelet and its complex-conjugate time-reverse share the same autocorrelation and spectrum. Let us verify this for simple two-point time functions. The spectrum of (b0, b1) is
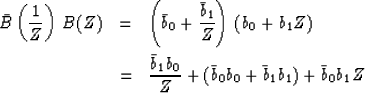 |
||
| (1) |
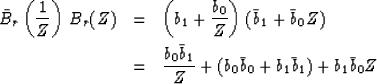 |
||
| (2) |
| |
(3) |
| |
(4) |
Now, what can we do to change the wavelet (3)
which will leave its spectrum (4) unchanged?
Clearly, b2 may be multiplied by any complex number of unit magnitude.
What is left of (4) can be broken
up into a product of factors of form ![]() .But such a factor is just like (3).
The time function of (Zi - Z) is (Zi, -1),
and its complex-conjugate time-reverse is
.But such a factor is just like (3).
The time function of (Zi - Z) is (Zi, -1),
and its complex-conjugate time-reverse is ![]() .In a generalization of (3) there could be N factors
.In a generalization of (3) there could be N factors
![]() .Any combination of them could be reversed.
Hence there are 2N different
wavelets which may be formed by reversals,
and all of the wavelets have the same spectrum.
Let us look off the unit circle in the complex plane.
The factor (Zi - Z) means that Zi is a root of both B(Z) and R(Z).
If we replace (Zi - Z) by
.Any combination of them could be reversed.
Hence there are 2N different
wavelets which may be formed by reversals,
and all of the wavelets have the same spectrum.
Let us look off the unit circle in the complex plane.
The factor (Zi - Z) means that Zi is a root of both B(Z) and R(Z).
If we replace (Zi - Z) by ![]() in B(Z),
we have removed
a root at Zi from B(Z) and replaced it by another at
in B(Z),
we have removed
a root at Zi from B(Z) and replaced it by another at ![]() .The roots of R(Z) have not changed a bit because there were originally roots
at both Zi and
.The roots of R(Z) have not changed a bit because there were originally roots
at both Zi and ![]() and the reversal has merely switched them
around.
Summarizing the situation in the complex plane, B(Z) has roots Zi
which occur anywhere,
R(Z) must have all the roots Zi and, in addition,
the roots
and the reversal has merely switched them
around.
Summarizing the situation in the complex plane, B(Z) has roots Zi
which occur anywhere,
R(Z) must have all the roots Zi and, in addition,
the roots ![]() .Replacing some particular root Zi by
.Replacing some particular root Zi by ![]() changes B(Z) but not R(Z).
The operation of replacing a root at Zi by
one at
changes B(Z) but not R(Z).
The operation of replacing a root at Zi by
one at ![]() may be written as
may be written as
| |
(5) |
Now let us discuss the calculation of B(Z) from a given R(Z).
First, the roots of R(Z) are by definition the solutions to R(Z) = 0.
If we multiply R(Z) by ZN (where R(Z) has been given up to degree N),
then
ZN R(Z) is a polynomial and the solutions Zi to ZN R(Z) = 0 will
be the same as the solutions of R(Z) = 0.
Finding all roots of a polynomial is a standard though difficult task.
Assuming this to have been done we may
then check to see if the roots come in the pairs Zi and ![]() .If they do not,
the R(Z) was not really a spectrum.
If they do, then for every zero inside the unit circle,
we must have one outside.
Refer to Figure 1.
.If they do not,
the R(Z) was not really a spectrum.
If they do, then for every zero inside the unit circle,
we must have one outside.
Refer to Figure 1.
|
3-1
Figure 1 Roots of | 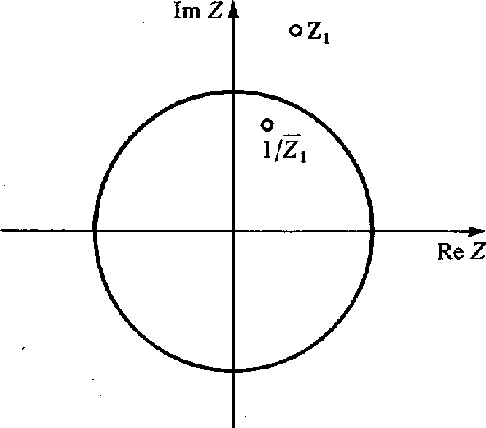 |
Thus, if we decide to make B(Z) be a minimum-phase wavelet with the spectrum R(Z), we collect all of the roots outside the unit circle. Then we create B(Z) with
| |
(6) |
This then summarizes the calculation of a minimum-phase wavelet from a given spectrum. When N is large, it is computationally very awkward compared to methods yet to be discussed. The value of the root method is that it shows certain basic principles.
The root method of spectral factorization was apparently developed by economists in the 1920s and 1930s. A number of early references may be found in Wold's book, Stationary Time Series.