




Next: THE CENTRAL-LIMIT THEOREM
Up: Resolution
Previous: FREQUENCY-STATISTICAL RESOLUTION
Many time functions are not completely random from point to point but become
more random when viewed over a longer time scale.
A popular mathematical
model embodying this concept is to make a so-called stationary time
series by putting random numbers into a filter as depicted in Figure 5.
The input xt may be independent random numbers or white
light.
[The two terms mean nearly the same thing in practice but the first
term is the stronger;
it means that xt is in no way related to xs if
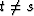 , whereas white light means that E(xt xs) = 0 if
, whereas white light means that E(xt xs) = 0 if 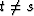 .]
The output random time series yt may vary rather slowly from point to
point if ft is a low-pass filter.
This is the usual case when we are
modeling continuous time functions.
The random time series may be called a
stationary random time series if neither the filter nor any property of
the random numbers (such as m or
.]
The output random time series yt may vary rather slowly from point to
point if ft is a low-pass filter.
This is the usual case when we are
modeling continuous time functions.
The random time series may be called a
stationary random time series if neither the filter nor any property of
the random numbers (such as m or  ) vary with time.
Stationarity is often assumed even wwhere it cannot be strictly true.
) vary with time.
Stationarity is often assumed even wwhere it cannot be strictly true.
This model will be useful later when we consider the problem of predicting
a future point on yt from knowledge of past values.
Now we will use the model to examine the estimation of the spectrum
of yt given a sample of n points of yt.
To begin with, we have a very precise meaning for
the spectrum of yt.
We have
| 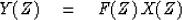 |
(49) |
and its conjugate
| 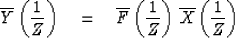 |
(50) |
Multiplying (49) by (50) we get
| 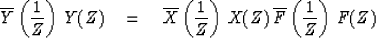 |
(51) |
but, from the previous section, we learned that 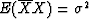 .Considering
.Considering 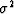 to be unity,
we see that the expected power spectrum of
the output Y is the energy spectrum of the filter F.
The overall situation is depicted in Figure 6.
The interesting question is how well
can we estimate the spectrum when we start with an n-point sample of yt.
We will describe three computationally different methods,
all having the same fundamental limitations.
4-5
to be unity,
we see that the expected power spectrum of
the output Y is the energy spectrum of the filter F.
The overall situation is depicted in Figure 6.
The interesting question is how well
can we estimate the spectrum when we start with an n-point sample of yt.
We will describe three computationally different methods,
all having the same fundamental limitations.
4-5
Figure 6 Spectral estimation.
 4-6
4-6
Figure 7 Spectral estimate of a random series.

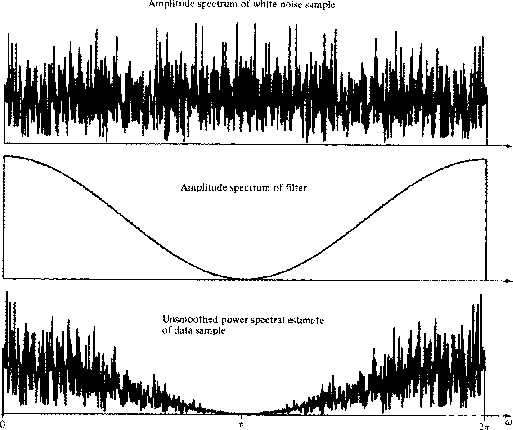
The first method uses a bank of filters as shown in Figure 7.
When random numbers excite the narrowband filter,
the output is somewhat like a sine wave.
It differs in one important respect.
A sine wave has constant amplitude,
but the output of a narrowband filter has an amplitude which
swings over a range.
This is illustrated in Figure 8.
If the bandwidth is narrow,
the amplitude changes slowly.
If the impulse response of the filter
has duration 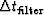 ,then the output amplitude at time t
will be randomly related to the amplitude at time
,then the output amplitude at time t
will be randomly related to the amplitude at time 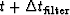 .Thus, in statistical averaging,
it is not the number of time points but the
number of intervals
.Thus, in statistical averaging,
it is not the number of time points but the
number of intervals 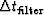 which enhance the reliability of the average.
Consequently, the decay time of the integrator
which enhance the reliability of the average.
Consequently, the decay time of the integrator 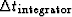 will generally be chosen to be greater than
will generally be chosen to be greater than
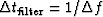 .The variability
.The variability 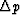 of the output p decreases
as
of the output p decreases
as 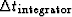 increases.
Since
vt has independent values over time spans
of about
increases.
Since
vt has independent values over time spans
of about 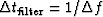 ,then the ``degrees of freedom'' smoothed over can be written
,then the ``degrees of freedom'' smoothed over can be written
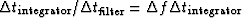 .The variability
.The variability 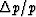 is proportional to the inverse
square root of the number of degrees of freedom,
and so we get
is proportional to the inverse
square root of the number of degrees of freedom,
and so we get
4-7
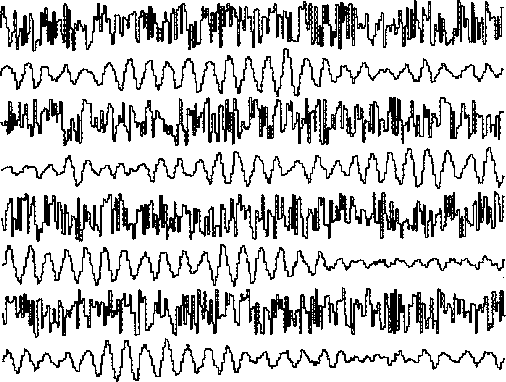
Figure 8 1024 random numbers before and after
narrowband filtering.
The filter was 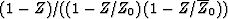 where
where 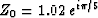 .
.

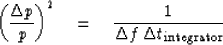
or, introducing the usual inequality,
| 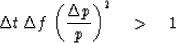 |
(52) |
The inequality (52) indicates the three-parameter uncertainty which
is fundamental to estimating power spectra of random functions. Two other
methods of estimating the spectrum of yt from a sample of length n
are exactly the same as the methods described in Sec. 4-3 as ways of
estimating the spectrum of white light.
In fact, (52) turns out to
be the same as (48).
The usual interpretation is that to attain a frequency resolution of
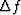 and a relative accuracy of
and a relative accuracy of 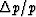 a time sample of duration
at least
a time sample of duration
at least ![$\Delta t \gt 1/[\Delta f\, (\Delta p/p)^2]$](img131.gif) will be required.
Although this sort of interpretation is generally correct,
it will break down for highly resonant series recorded for a short time.
Then the data sample
may be predictable an appreciable distance off its ends so that the effective
will be required.
Although this sort of interpretation is generally correct,
it will break down for highly resonant series recorded for a short time.
Then the data sample
may be predictable an appreciable distance off its ends so that the effective
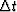 is somewhat (perhaps appreciably) larger than the sample length.
is somewhat (perhaps appreciably) larger than the sample length.
EXERCISES:
- It is popular to taper the ends of a data sample so that the data go
smoothly to zero at the ends of the sample.
Choose a weighting function and
discuss in a semiquantitative fashion its effect on
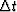 ,
, 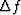 ,and
,and 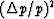 .
. - Answer the question of Exercise 1,
where the autocorrelation function
is tapered rather than the data sample.





Next: THE CENTRAL-LIMIT THEOREM
Up: Resolution
Previous: FREQUENCY-STATISTICAL RESOLUTION
Stanford Exploration Project
10/30/1997

![]() ,then the output amplitude at time t
will be randomly related to the amplitude at time
,then the output amplitude at time t
will be randomly related to the amplitude at time ![]() .Thus, in statistical averaging,
it is not the number of time points but the
number of intervals
.Thus, in statistical averaging,
it is not the number of time points but the
number of intervals ![]() which enhance the reliability of the average.
Consequently, the decay time of the integrator
which enhance the reliability of the average.
Consequently, the decay time of the integrator ![]() will generally be chosen to be greater than
will generally be chosen to be greater than
![]() .The variability
.The variability ![]() of the output p decreases
as
of the output p decreases
as ![]() increases.
Since
vt has independent values over time spans
of about
increases.
Since
vt has independent values over time spans
of about ![]() ,then the ``degrees of freedom'' smoothed over can be written
,then the ``degrees of freedom'' smoothed over can be written
![]() .The variability
.The variability ![]() is proportional to the inverse
square root of the number of degrees of freedom,
and so we get
is proportional to the inverse
square root of the number of degrees of freedom,
and so we get
![]()
![]() and a relative accuracy of
and a relative accuracy of ![]() a time sample of duration
at least
a time sample of duration
at least ![]() will be required.
Although this sort of interpretation is generally correct,
it will break down for highly resonant series recorded for a short time.
Then the data sample
may be predictable an appreciable distance off its ends so that the effective
will be required.
Although this sort of interpretation is generally correct,
it will break down for highly resonant series recorded for a short time.
Then the data sample
may be predictable an appreciable distance off its ends so that the effective
![]() is somewhat (perhaps appreciably) larger than the sample length.
is somewhat (perhaps appreciably) larger than the sample length.