




Next: About this document ...
Up: Resolution
Previous: THE CENTRAL-LIMIT THEOREM
It is always important to have some idea of the size and influence of
random errors.
It is often important to be able to communicate this
idea to others in the form of a statement such as
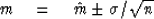
In a matter of any controversy you may be called upon to define a probability
that the true mean lies in your stated interval; in other words, what is
your confidence that m lies in the interval
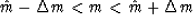
Before you can answer questions about probability,
it is necessary to make
some assumptions and assertions about the probability functions which
control your random errors.
The assertion that errors are independent of
one another is your most immediate hazard.
If they are not, as is often the case,
you may be able to readjust the numerical value of n to be an
estimate of the number of independent errors.
We did something like this
in time series analysis when we took n to be not the number of points
on the time series but the number of intervals of length
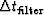 .The second big hazard in trying to state a confidence interval is
the common assumption that,
because of the central-limit theorem and for
lack of better information,
the errors follow a gaussian probability function.
If in fact the data errors include blunders which arise from human errors or
blunders from transient electronic equipment difficulties,
then the
gaussian assumption can be very wrong and can lead you into serious errors in
geophysical interpretation.
Some useful help is found in the field of nonparametric statistics.
.The second big hazard in trying to state a confidence interval is
the common assumption that,
because of the central-limit theorem and for
lack of better information,
the errors follow a gaussian probability function.
If in fact the data errors include blunders which arise from human errors or
blunders from transient electronic equipment difficulties,
then the
gaussian assumption can be very wrong and can lead you into serious errors in
geophysical interpretation.
Some useful help is found in the field of nonparametric statistics.
To begin with, it is helpful to rephrase the original question into one
involving the median rather than the mean.
The median m1 is defined as that
value which is expected to be less than half of the population and
greater than the other half.
In many--if not most--applications the
median is a ready,
practical substitute for the arithmetic mean.
The median is insensitive to a data point,
which, by some blunder, is near infinity.
In fact,
median and mean are equal when the probability function is symmetrical.
For a sample of n numbers 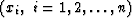 ,the median m1 may be estimated by reordering the numbers from smallest
to largest and then selecting the number in the middle as the estimate of
the median
,the median m1 may be estimated by reordering the numbers from smallest
to largest and then selecting the number in the middle as the estimate of
the median 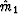 .Specifically, let the recordered xi be denoted
by xi' where
.Specifically, let the recordered xi be denoted
by xi' where 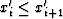 .Then we have
.Then we have 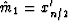 .Now it turns out that without knowledge of the probability
density function for the random variables xi we will still be able to
compute the probability that the true median m1 is contained in the interval
.Now it turns out that without knowledge of the probability
density function for the random variables xi we will still be able to
compute the probability that the true median m1 is contained in the interval
| 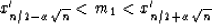 |
(71) |
For example, set 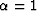 and N = 100, the assertion is that we can now
calculate the probability that the true median m1 lies between the 40th
and the 60th percentile of our data.
The trick is this: Define a new random variable
and N = 100, the assertion is that we can now
calculate the probability that the true median m1 lies between the 40th
and the 60th percentile of our data.
The trick is this: Define a new random variable
| 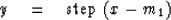 |
(72) |
The step function equals +1 if x > m1 and equals if x < m1.
The new random variable y takes on only values of zero and one with equal
probability;
thus we know its probability function even though we may not
know the probability function for the random variable x.
Now define a third random variable s as
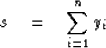
Since each yi is zero or one,
then s must be an integer between zero and n.
Further more, the probability that s takes the value
j is given by the coefficient of Zj of 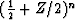 .
Now the probability that s lies in the interval
.
Now the probability that s lies in the interval
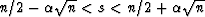 is readily determined by adding the
required coefficients of Zj,
and this probability is by definition
equal to the probability that the median m1 lies in the interval
(71).
For
is readily determined by adding the
required coefficients of Zj,
and this probability is by definition
equal to the probability that the median m1 lies in the interval
(71).
For 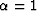 and large n this probability works
out to about 95 percent.
and large n this probability works
out to about 95 percent.





Next: About this document ...
Up: Resolution
Previous: THE CENTRAL-LIMIT THEOREM
Stanford Exploration Project
10/30/1997
![]()
![]()
![]() ,the median m1 may be estimated by reordering the numbers from smallest
to largest and then selecting the number in the middle as the estimate of
the median
,the median m1 may be estimated by reordering the numbers from smallest
to largest and then selecting the number in the middle as the estimate of
the median ![]() .Specifically, let the recordered xi be denoted
by xi' where
.Specifically, let the recordered xi be denoted
by xi' where ![]() .Then we have
.Then we have ![]() .Now it turns out that without knowledge of the probability
density function for the random variables xi we will still be able to
compute the probability that the true median m1 is contained in the interval
.Now it turns out that without knowledge of the probability
density function for the random variables xi we will still be able to
compute the probability that the true median m1 is contained in the interval
![]()