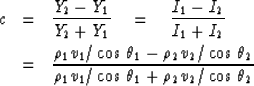Next: SOURCE-RECEIVER RECIPROCITY
Up: Mathematical physics in stratified
Previous: NUMERICAL MATRIZANTS
We have seen a host of examples of how physical problems
in stratified source-free media reduce to the form
| 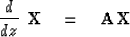 |
(1) |
Where 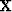 is a vector of physical variables
and
is a vector of physical variables
and 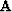 is a matrix which depends on z
if material properties depend upon z.
An important set of new variables in the vector
is a matrix which depends on z
if material properties depend upon z.
An important set of new variables in the vector 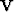 is defined by multiplying the vector of physical variables
is defined by multiplying the vector of physical variables 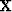 by a square matrix
by a square matrix 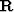
| 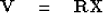 |
(2) |
where 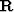 is the matrix of row eigenvectors of the matrix
is the matrix of row eigenvectors of the matrix 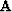 .Inverse to
.Inverse to 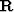 is the matrix
is the matrix 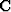 of column eigenvectors of
of column eigenvectors of 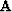 .Premultiplying (9-3-2) by
.Premultiplying (9-3-2) by 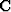 and using
and using 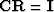 we get the inverse relation to (9-3-2)
which is useful to find the physical variables
we get the inverse relation to (9-3-2)
which is useful to find the physical variables 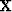 from the new variables
from the new variables 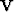 .
.
| 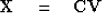 |
(3) |
Inserting (9-3-3) into (9-3-1) we obtain
| 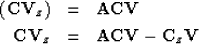 |
(4) |
| (5) |
Premultiplying by 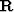 and using
and using 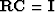 we obtain
we obtain
| 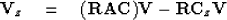 |
(6) |
Since we have supposed 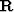 and
and 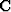 to be row and column eigenvector matrices of
to be row and column eigenvector matrices of 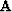 we can replace
we can replace 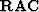 by the diagonal matrix
of eigenvalues
by the diagonal matrix
of eigenvalues 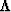 ,that is
,that is
| 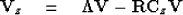 |
(7) |
In any region of physical space where the material is homogeneous
then 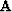 , hence
, hence 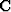 ,will be independent of z and (9-3-5) will reduce to
,will be independent of z and (9-3-5) will reduce to
| 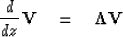 |
(8) |
But the only matrix in (9-3-6) is a diagonal matrix,
and so the problem for the different variables in the vector 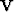 decouples into a separate problem for each component.
In wave problems it will be seen to be appropriate
to call the components of
decouples into a separate problem for each component.
In wave problems it will be seen to be appropriate
to call the components of 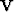 upgoing and downgoing wave variables.
These variables flow up and down in homogeneous regions
without interacting with each other.
Let us consider an example.
upgoing and downgoing wave variables.
These variables flow up and down in homogeneous regions
without interacting with each other.
Let us consider an example.
In Sec. 9-1 we deduced that the matrix first-order differential equation for
the acoustic problem in a region of no sources takes the form
| ![\begin{displaymath}
\frac{d}{dz}\left[ \begin{array}
{c} P \\ W \end{array} \ri...
...right]\,
\left[ \begin{array}
{c} P \\ W \end{array} \right] \end{displaymath}](img80.gif) |
(9) |
where
| 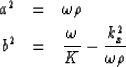 |
(10) |
| (11) |
The matrix of column eigenvectors 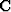 and the matrix of row eigenvectors of the matrix of (9-3-7) are readily verified to be
and the matrix of row eigenvectors of the matrix of (9-3-7) are readily verified to be
| ![\begin{eqnarray}
\mbox{\bf C} &=& \left[ \begin{array}
{rc} 1 & 1 \vspace{.1in}\...
... -\frac{a}{b} \vspace{.1in}\\ 1 & \frac{a}{b} \end{array} \right]\end{eqnarray}](img82.gif) |
(12) |
| (13) |
It is also readily verified that the vectors are normalized,
namely 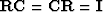 and that
and that
![\begin{displaymath}
\Lambda \eq \mbox{\bf RAC} \eq \left[ \begin{array}
{cc} -iab & 0 \vspace{.1in}\\ 0 &+iab \end{array} \right] \end{displaymath}](img84.gif)
The downgoing wave variable D
is associated with the iab eigenvalue
and the upcoming wave variable U is associated with the -iab.
We have definitions for up- and downgoing waves as
| ![\begin{displaymath}
\left[ \begin{array}
{c} U \\ D \end{array} \right] \eq \fr...
...y} \right] \left[ \begin{array}
{c} P \\ W \end{array} \right]\end{displaymath}](img85.gif) |
(1) |
Of course a row eigenvector may contain an arbitrary multiplicative scaling factor if the scaling factor is divided from the corresponding column eigenvector.
This means that the definition (9-3-12a) is not unique.
As it happens,
the present scale factors give the up- and downgoing waves the physical dimensions of P.
The physical variables P and W are found from U and D by the inverse relation
| ![\begin{displaymath}
\left[ \begin{array}
{c} P \\ W \end{array} \right] \eq \le...
...\right] \; \left[ \begin{array}
{c} U \\ D \end{array} \right]\end{displaymath}](img86.gif) |
(2) |
from which we see that the pressure P is the downgoing wave plus the upcoming wave and the vertical velocity is b/a times the difference.
Equation (9-3-5) governing the propagation of U and D is
| ![\begin{displaymath}
\frac{d}{dz} \left[ \begin{array}
{c} U \\ D \end{array} \r...
... \right]\, \left[ \begin{array}
{c} U \\ D \end{array} \right]\end{displaymath}](img87.gif) |
(13) |
In any region of space where b/a is not a function of z
we are left with the simple uncoupled equations
| ![\begin{displaymath}
\frac{d}{dz} \left[ \begin{array}
{c} U \\ D \end{array} \r...
... \right]\, \left[ \begin{array}
{c} U \\ C \end{array} \right]\end{displaymath}](img88.gif) |
(14) |
Strictly, to justify the definitions of U and D as up- and downgoing waves
we will have to be sure that the downgoing solution takes the form
| 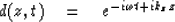 |
(15) |
where 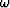 and kz must agree in sign
so that constant phase is maintained as both z and t increase.
The opposite sign must apply to U.
In other words kz = ab must take the sign of
and kz must agree in sign
so that constant phase is maintained as both z and t increase.
The opposite sign must apply to U.
In other words kz = ab must take the sign of 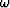 .To see that this happens we take the square root of the product
of (9-3-8) and (9-3-9).
.To see that this happens we take the square root of the product
of (9-3-8) and (9-3-9).
| 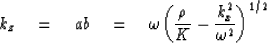 |
(16) |
For vertically propagating waves we have kx = 0
so that kz = ab specializes to
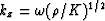 .Substituting this value into (9-3-15),
we see that the phase angle of the exponential is constant if
.Substituting this value into (9-3-15),
we see that the phase angle of the exponential is constant if
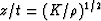 ,making it clear that the material's intrinsic velocity is given by
,making it clear that the material's intrinsic velocity is given by
| 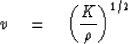 |
(17) |
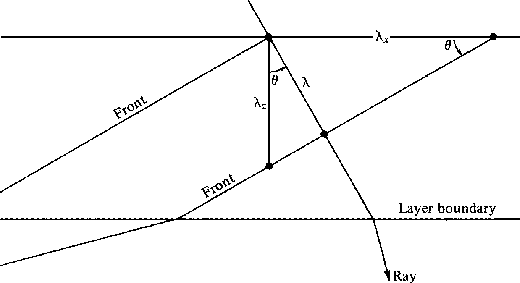
Reference to Figure 9-1 shows that the angle 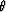 between the vertical and a ray is defined by
between the vertical and a ray is defined by
| 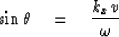 |
(18) |
Inserting (9-3-17) and (9-3-18) into (9-3-16) we obtain
| 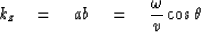 |
(19) |
9-1
Figure 1
Rays and wavefronts in a layer.
The wavelength 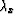 seen on the x axis
and the wavelength
seen on the x axis
and the wavelength 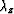 seen on the z axis
are both greater than the wavelength
seen on the z axis
are both greater than the wavelength 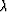 seen along the ray.
Clearly,
seen along the ray.
Clearly,
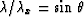 and
and 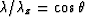 so the spatial frequencies
so the spatial frequencies 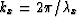 and
and 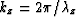 satisfy
satisfy 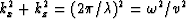 , which, besides being the Pythagorean theorem
(since
, which, besides being the Pythagorean theorem
(since 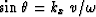 ),
is the Fourier transform of the wave equation.
Snell's law that
),
is the Fourier transform of the wave equation.
Snell's law that 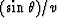 is the same from layer to layer is thus equivalent to saying that
is the same from layer to layer is thus equivalent to saying that
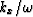 is the same in each layer.
That the spatial frequency kx is the same constant in each layer
is essential to the satisfaction of continuity conditions
at the layer interfaces.
is the same in each layer.
That the spatial frequency kx is the same constant in each layer
is essential to the satisfaction of continuity conditions
at the layer interfaces.

The time function (9-3-15) is complex.
To get a real time function the expression (9-3-15) must be summed
or integrated to include both positive and negative frequencies.
Then, as we saw in the chapters on time series analysis,
we must have 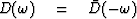 .
.
The quantity b/a will turn out
to be the material's characteristic admittance Y.
Taking the square root of the ratio of (9-3-9) over (9-3-8) we have
| 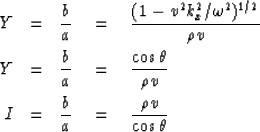 |
(20) |
| (21) |
| (22) |
We shall now verify that this definition of impedance
is the same as the one in the previous chapter.
To do this we take a careful look at the matrizant
to cross a layer
![$\mbox{\rm exp}[\mbox{\bf A}_{1}(z_{2} - z_{1}] = \mbox{\rm exp}(\mbox{\bf A}\, \triangle z)$](img111.gif) .By Sylvester's theorem we have for the matrizant
.By Sylvester's theorem we have for the matrizant
| ![\begin{displaymath}
\mbox{\rm exp}(\mbox{\bf A}\, \triangle z) = \mbox{\bf C}\le...
... 0 & e^{+ik_{z}\; \triangle z} \end{array} \right]\mbox{\bf R}\end{displaymath}](img112.gif) |
(23) |
The matrizant relates the wave variables at the top z1 of a layer to those
at the bottom z2.
Thus (9-3-23) enables us to write
| ![\begin{displaymath}
\left[ \begin{array}
{c} P \\ W \end{array} \right]_{2} \eq...
..._{1}\, \left[ \begin{array}
{c} P \\ W \end{array} \right]_{1}\end{displaymath}](img113.gif) |
(24) |
Equation (9-3-24) which seems to have jumped at us from the mysteries of Sylvester's theorem actually has a simple interpretation.
Starting on the right, we interpret the multiplication of 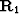 into the P and W variables as a conversion to up- and downgoing variables.
Then the multiplication by
into the P and W variables as a conversion to up- and downgoing variables.
Then the multiplication by
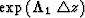 carries these across the layer and the multiplication
by
carries these across the layer and the multiplication
by 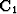 converts back to P and W variables
which are continuous crossing an interface.
Multiplying (9-3-24) through by R2
and noting (9-3-11) and (9-3-12) we have
converts back to P and W variables
which are continuous crossing an interface.
Multiplying (9-3-24) through by R2
and noting (9-3-11) and (9-3-12) we have
| ![\begin{displaymath}
\left[ \begin{array}
{c} U \\ D \end{array} \right]_{2} \eq...
...ngle z)\left[ \begin{array}
{c} U \\ D \end{array} \right]_{1}\end{displaymath}](img117.gif) |
(25) |
In (9-3-25) we have now defined the up- and downgoing waves
just beneath the interface as we did in the previous chapter.
We should now be able to recognize the matrix as having the same form. It is
| ![\begin{displaymath}
\frac{1}{2}\left[ \begin{array}
{rr} 1 & -\frac{1}{Y_{2}} \v...
...angle z} & 0 \\ 0 & e^{iab \; \triangle z} \end{array} \right]\end{displaymath}](img118.gif) |
(26) |
Defining the Z transform variable by
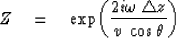
Now we recognize that the travel time across the layer is 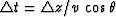 . The layer matrix (9-3-26) is
. The layer matrix (9-3-26) is
| ![\begin{displaymath}
\frac{Y_{1} + Y_{2}}{2Y_{2}}\left[ \begin{array}
{cc}
1 & ...
...\begin{array}
{cc} Z^{-1/2} & \\ & Z^{1/2} \end{array} \right]\end{displaymath}](img121.gif) |
(27) |
which may be compared to the matrix of (8-2-4) namely,
![\begin{displaymath}
\frac{1}{t}\, \left[ \begin{array}
{cc} 1 & c \\ c & 1 \end...
...n{array}
{cc} Z^{-1/2} & 0 \\ 0 & Z^{1/2} \end{array} \right] \end{displaymath}](img122.gif)
establishing that the definition Y = b/a has led to the familiar definition of reflection coefficient
| 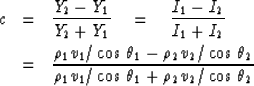 |
|
| (28) |
EXERCISES:
-
Redefine the eigenvectors so that W + D + U and P = (D - U)/Y.
This transformation would be useful if we wanted t = 1 + c to refer
to vertical velocity normalized variables
instead of pressure variables as in Chap. 8.
Deduce changes to all the equations of this section.
-
Write the matrizant which crosses a layer in terms of a, b, and layer thickness h.





Next: SOURCE-RECEIVER RECIPROCITY
Up: Mathematical physics in stratified
Previous: NUMERICAL MATRIZANTS
Stanford Exploration Project
10/30/1997
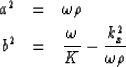
![]() and the matrix of row eigenvectors of the matrix of (9-3-7) are readily verified to be
and the matrix of row eigenvectors of the matrix of (9-3-7) are readily verified to be
![\begin{eqnarray}
\mbox{\bf C} &=& \left[ \begin{array}
{rc} 1 & 1 \vspace{.1in}\...
... -\frac{a}{b} \vspace{.1in}\\ 1 & \frac{a}{b} \end{array} \right]\end{eqnarray}](img82.gif)
![\begin{displaymath}
\Lambda \eq \mbox{\bf RAC} \eq \left[ \begin{array}
{cc} -iab & 0 \vspace{.1in}\\ 0 &+iab \end{array} \right] \end{displaymath}](img84.gif)
![\begin{displaymath}
\left[ \begin{array}
{c} U \\ D \end{array} \right] \eq \fr...
...y} \right] \left[ \begin{array}
{c} P \\ W \end{array} \right]\end{displaymath}](img85.gif)
![\begin{displaymath}
\left[ \begin{array}
{c} P \\ W \end{array} \right] \eq \le...
...\right] \; \left[ \begin{array}
{c} U \\ D \end{array} \right]\end{displaymath}](img86.gif)
![]() .
.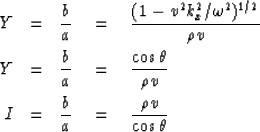
![]() .By Sylvester's theorem we have for the matrizant
.By Sylvester's theorem we have for the matrizant
![\begin{displaymath}
\mbox{\rm exp}(\mbox{\bf A}\, \triangle z) = \mbox{\bf C}\le...
... 0 & e^{+ik_{z}\; \triangle z} \end{array} \right]\mbox{\bf R}\end{displaymath}](img112.gif)
![\begin{displaymath}
\frac{1}{2}\left[ \begin{array}
{rr} 1 & -\frac{1}{Y_{2}} \v...
...angle z} & 0 \\ 0 & e^{iab \; \triangle z} \end{array} \right]\end{displaymath}](img118.gif)
![]()
![\begin{displaymath}
\frac{Y_{1} + Y_{2}}{2Y_{2}}\left[ \begin{array}
{cc}
1 & ...
...\begin{array}
{cc} Z^{-1/2} & \\ & Z^{1/2} \end{array} \right]\end{displaymath}](img121.gif)
![]()