




Next: Variance of the sample
Up: TIME-STATISTICAL RESOLUTION
Previous: Probability and independence
Now let xt be a time series made up of identically distributed
random numbers: mx and  do not depend on time.
Let us also suppose that they are independently chosen; this
means in particular that for any different times t and s (
do not depend on time.
Let us also suppose that they are independently chosen; this
means in particular that for any different times t and s (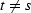 ):
):
| 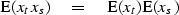 |
(13) |
Suppose we have a sample of n points of xt and are
trying to determine the value of mx.
We could make an estimate  of the mean mx with the formula
of the mean mx with the formula
| 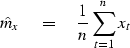 |
(14) |
A somewhat more elaborate method of estimating the mean
would be to take a weighted average.
Let wt define a set of weights normalized so that
| 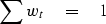 |
(15) |
With these weights, the more elaborate estimate 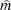 of the mean is
of the mean is
| 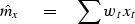 |
(16) |
Actually (14) is just a special case of (16);
in (14) the
weights are wt = 1/n.
Further, the weights could be convolved on the random time series,
to compute local averages of this time series, thus smoothing it.
The weights are simply a filter response where the filter coefficients happen
to be positive and cluster together.
Figure 6 shows an example: a random walk function
with itself smoothed locally.
walk
Figure 6
Random walk and itself smoothed (and shifted downward).






Next: Variance of the sample
Up: TIME-STATISTICAL RESOLUTION
Previous: Probability and independence
Stanford Exploration Project
3/1/2001
