




Next: Tau tomography
Up: THEORY
Previous: Smoothing slowness rather than
The proposed regularized tomography problem still has the problem
of slow convergence. By reformulating the problem in helix space
Claerbout (1998c), we can take advantage of 1-D theory to change our
regularized problem into a preconditioned one. We start by defining
a new variable 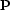 :
:
| 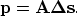 |
(6) |
By applying polynomial division to our steering filters, we can
create 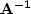 which becomes a smoothing operator.
We can then rewrite our fitting goals as
which becomes a smoothing operator.
We can then rewrite our fitting goals as
| 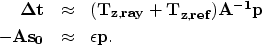 |
|
| (7) |





Next: Tau tomography
Up: THEORY
Previous: Smoothing slowness rather than
Stanford Exploration Project
4/20/1999
![]() which becomes a smoothing operator.
We can then rewrite our fitting goals as
which becomes a smoothing operator.
We can then rewrite our fitting goals as