Next: Smoothing slowness rather than
Up: Clapp & Biondi: Velocity
Previous: INTRODUCTION
Following the method described in Clapp 1998,
we began by linearizing the tomography problem around an initial
guess at our slowness model 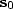 . We assumed ray stationarity
and described the change in travel time (
. We assumed ray stationarity
and described the change in travel time (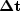 ) as being linearly
related to our change in slowness (
) as being linearly
related to our change in slowness (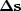 ):
):
| 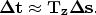 |
(1) |
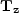 is composed of two portions. The first,
is composed of two portions. The first, 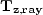 simply
applies
simply
applies
| 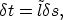 |
(2) |
or that the change in the travel time is (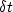 ) is equal to change in
slowness (
) is equal to change in
slowness (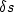 ) times length of the ray of the ray segment (
) times length of the ray of the ray segment (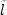 ) of the ray
connecting the source, reflector, and the receiver.
The second component,
) of the ray
connecting the source, reflector, and the receiver.
The second component, 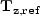 , can be thought of as a chain of two
operators: the first maps our change in slowness (
, can be thought of as a chain of two
operators: the first maps our change in slowness (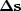 ) into reflector
movement, the second maps the reflector movement into our change in travel
times (
) into reflector
movement, the second maps the reflector movement into our change in travel
times (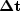 ) van Trier (1990). This second term amounts to performing
residual migration and can be done by back projecting a ray located
at the reflection point perpendicular to the reflector Stork (1994),
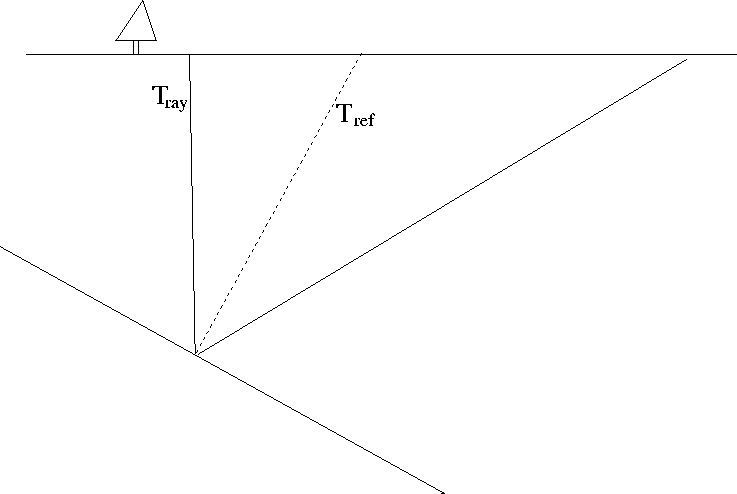
Figure 1. Taking both components into account our
tomography fitting goal becomes
) van Trier (1990). This second term amounts to performing
residual migration and can be done by back projecting a ray located
at the reflection point perpendicular to the reflector Stork (1994),
Figure 1. Taking both components into account our
tomography fitting goal becomes
| 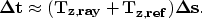 |
(3) |
schematic
Figure 1 The two portions of the back
projection operator. 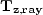 is the pair of rays through
is the pair of rays through
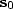 from the source to the
receiver that obey Snell's law at the reflector.
from the source to the
receiver that obey Snell's law at the reflector.  is the raypath
from this reflection point to the surface.
is the raypath
from this reflection point to the surface.






Next: Smoothing slowness rather than
Up: Clapp & Biondi: Velocity
Previous: INTRODUCTION
Stanford Exploration Project
4/20/1999