3-D Kolmogoroff spectral factorization

A simple linear model for the observed solar oscillations consists of a convolution of a source function with the impulse response of the sun's surface. The source function is stochastic in nature, and may be characterized as being spectrally white in time and space with random phase. The impulse response contains the spectral color, and is commonly a minimum-phase function.

If this model holds true, then estimating the source function reduces to estimating a minimum-phase function with the same (w,k_x,k_y) spectrum as the original data: multi-dimensional spectral factorization.

Helical boundary conditions Claerbout (1998) provide a framework for converting a multi-dimensional problem into an equivalent problem in only one dimension, and allow us to solve the three-dimensional spectral factorization problem efficiently.

We perform the spectral factorization rapidly in the frequency domain in three steps. Firstly, we transform the multi-dimensional signal to an equivalent one-dimensional signal using helical boundary conditions. Secondly, we perform one-dimensional spectral factorization with Kolmogoroff's 1939 algorithm. Finally, we remap the impulse response back to three-dimensional space. We reduce wrap-around effects by padding the spatial axes.

Figure 3 shows the impulse response derived from Kolmogoroff spectral factorization as a function of radial distance from the impulse. It looks very similar to the cross-correlation time-distance seismogram shown in Figure 4, and those displayed by Kosovichev (1999). However, for the dataset described above, this operation was approximately twenty times faster than cross-correlating every trace in either ($w,{\bf x}$) or ($t,{\bf x}$). The speed-up becomes apparent when you consider that cross-correlating every trace with every other trace requires $O(N_x^2 \; N_y^2 \; N_t)$operations, whereas one-dimensional spectral factorization requires only $O(N \log N)$ operations where N=N_x N_y N_t.

 

kolstack Figure 3 Impulse response derived by Kolmogoroff spectral factorization binned as a function of radial distance from the impulse.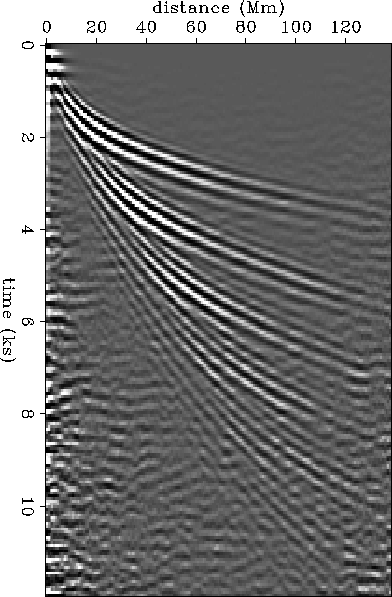

 

xcorr Figure 4 Impulse response derived by cross-correlation binned as a function of radial distance from the impulse. More noise is present in this Figure compared to Figure 3 because less data was used in the calculation.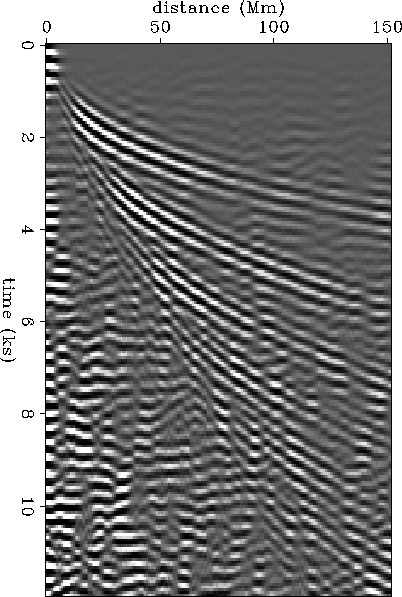

 

lmo
Figure 5 The top two panels show a shot gather from the Gulf of Mexico before (left) and after (right) linear moveout with the water velocity. The lower two panels show the solar impulse response before (left) and after (right) linear moveout at 10 km/s.