Boundaries and triplications

This section presents a short discussion of the special treatment required by the boundaries of the computation domain. These boundaries are of two kinds: exterior boundaries, represented by the edges of the computational domain, and interior boundaries, represented by the triplication lines. Because of the centered finite-difference scheme, HWT cannot be used at the boundaries of the computational domain. This means that the boundaries need to be treated differently from the rest of the domain. Also, the centered finite-difference scheme cannot be used when the wavefronts create triplications. Triplications represent points of discontinuity of the derivative along the wavefront, and, therefore, the centered finite-difference representation of the derivative is inappropriate. Figure 4 describes a point of triplication represented in both the physical (Cartesian) domain (left) and the ray coordinate domain (right).

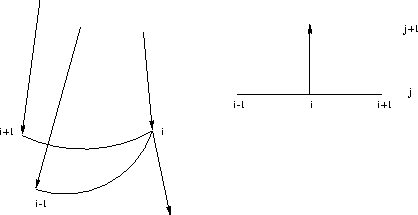One possible solution for the boundaries is to make a local approximation of the wavefront. Instead of considering the actual points on the wavefront, we can create an approximate wavefront that is locally orthogonal to the ray arriving at the cusp point, as depicted in Figure 5. We can then pick an appropriate number of points (two in 2-D or four in 3-D) on this approximate wavefront, and use the HWT scheme without any change. A new search for the cusp points is then needed on the new wavefront before we can proceed any further.

 

cusp Figure 4 The centered finite-difference representation of the derivative along the wavefront cannot be used at the cusps. These points represent discontinuities in the derivative, and need to be treated separately.

 

hrt Figure 5 The centered finite-difference representation of the derivative along the wavefront cannot be used at the cusps. Instead, we can use a local approximation of the wavefront as a plane locally orthogonal to the ray arriving at the cusp.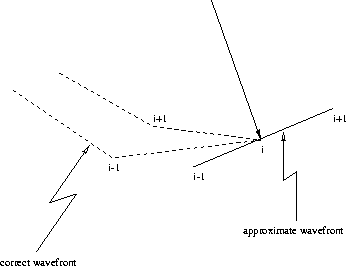