First I apply the enhanced helix derivative filter to some familiar
images and check the effects of adjustable parameters na and ![]() .
.
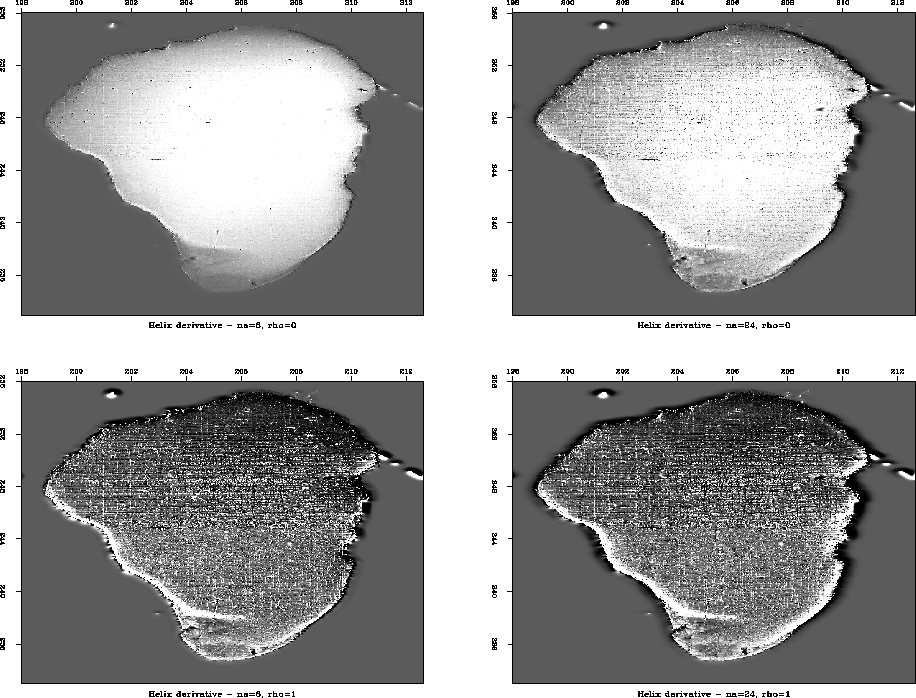
Figure 1 shows the views of the Sea of Galilee
created by helix derivative filters with different na and ![]() .The top two plots (with
.The top two plots (with ![]() ) indicate that as the half filter
length na increases, the contrast of the image increases. This
means the longer filter keeps less low frequency components, indicating
a lower zero-frequency response. The vertical plots (with same na)
indicate that as
) indicate that as the half filter
length na increases, the contrast of the image increases. This
means the longer filter keeps less low frequency components, indicating
a lower zero-frequency response. The vertical plots (with same na)
indicate that as ![]() increases, the contrast increases also, as
expected from the definition of the enhanced helix filter equation.
increases, the contrast increases also, as
expected from the definition of the enhanced helix filter equation.
To compare the properties of the filters with different na other
than the zero-frequency response, I set ![]() in the bottom two
plots, so that they have the same zero-frequency response. The plots
are very similar, and the difference between them is very weak.
in the bottom two
plots, so that they have the same zero-frequency response. The plots
are very similar, and the difference between them is very weak.
 |
As the examples above show, the zero-frequency response of the enhanced
helix derivative filter decreases as na or ![]() increases. Thus
filters with different na may create the same results by adjusting
increases. Thus
filters with different na may create the same results by adjusting
![]() , which provides the possibility of using a short filter instead
of a long filter in image processing and reduce the computational cost
greatly. By adjusting
, which provides the possibility of using a short filter instead
of a long filter in image processing and reduce the computational cost
greatly. By adjusting ![]() , the enhanced short filter can reach a low
level of zero-frequency response, which is done conventionally by using a
long filter.
, the enhanced short filter can reach a low
level of zero-frequency response, which is done conventionally by using a
long filter.
Since the short filter is equivalent to the long filter when adjusting
![]() , now
, now ![]() plays the key role in image processing for the
enhanced helix derivative filter, and na is not an important parameter.
When the high frequency component is too weak compared with the low
frequency, a large
plays the key role in image processing for the
enhanced helix derivative filter, and na is not an important parameter.
When the high frequency component is too weak compared with the low
frequency, a large ![]()
![]() should be chosen
in order resolve details in the image. Otherwise, a small
should be chosen
in order resolve details in the image. Otherwise, a small ![]() would
be suitable. Based on the balance of the computation cost and response
symmetry, I recommend the use of
would
be suitable. Based on the balance of the computation cost and response
symmetry, I recommend the use of ![]() .
.
From the quantitative analysis of spectra of the enhanced helix
derivative filter (see the appendix A), I can find ![]() according to
empirical formula
according to
empirical formula
| |
(4) |
For the view of the Sea of Galilee, the high frequency component is
very weak, so I chose I0=0.002, na=8, and ![]() . Figure
2 shows the preferred and gradient
roughened results.
. Figure
2 shows the preferred and gradient
roughened results.
 |