




Next: Born traveltime sensitivity
Up: Rickett: Traveltime sensitivity kernels
Previous: Introduction
A generic discrete linear inverse problem may be written as
| 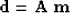 |
(1) |
where 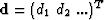 is the known data vector,
is the known data vector,
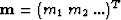 is the unknown model vector, and
is the unknown model vector, and  represents the linear
relationship between them.
A natural question to ask is: which parts of the
model influence a given observed data-point?
The answer is that the row of matrix,
represents the linear
relationship between them.
A natural question to ask is: which parts of the
model influence a given observed data-point?
The answer is that the row of matrix, 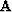 ,corresponding to the data-point of interest will be non-zero
where that point in model space influences the data-value.
Rows of
,corresponding to the data-point of interest will be non-zero
where that point in model space influences the data-value.
Rows of 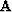 may therefore be thought of as sensitivity kernels,
describing which points in model space are sensed by a given
data-point.
may therefore be thought of as sensitivity kernels,
describing which points in model space are sensed by a given
data-point.
For a generic linearized traveltime tomography problem, traveltime
perturbations, 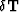 , are related to slowness
perturbations,
, are related to slowness
perturbations, 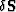 , through a linear system,
, through a linear system,
| 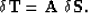 |
(2) |
The form of the sensitivity kernels depend on the the modeling
operator, 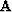 .
.
Under the ray-approximation, traveltime for a given ray, T, is
calculated by integrating slowness along the ray-path,
| 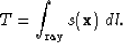 |
(3) |
Assuming that the ray-path is insensitive to a small slowness
perturbation, the perturbation in traveltime is
given by the path integral of the slowness perturbation along the ray,
| 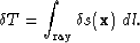 |
(4) |
Since traveltime perturbations given by equation (4)
are insensitive to slowness perturbations anywhere off the geometric
ray-path, the sensitivity kernel is identically zero everywhere in
space, except along the ray-path where it is constant.
The implication for ray-based traveltime tomography is that traveltime
perturbations should be back-projected purely along the ray-path.
We are interested in more accurate tomographic systems of the form
of equation (3), that model the effects of
finite-frequency wave-propagation more accurately than simple
ray-theory.
Once we have such an operator, the first question to ask is: what
do the rows look like?





Next: Born traveltime sensitivity
Up: Rickett: Traveltime sensitivity kernels
Previous: Introduction
Stanford Exploration Project
4/27/2000
![]() , are related to slowness
perturbations,
, are related to slowness
perturbations, ![]() , through a linear system,
, through a linear system,