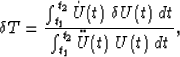Next: Rytov traveltime sensitivity
Up: Theory
Previous: Theory
One approach to building a linear finite-frequency traveltime operator
is to apply the first-order Born approximation, to obtain a linear
relationship between slowness perturbation, 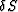 , and wavefield
perturbation,
, and wavefield
perturbation, 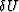 ,
,
| 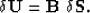 |
(5) |
The Born operator, 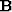 , is a discrete implementation of
equation (16), which is described in the Appendix.
, is a discrete implementation of
equation (16), which is described in the Appendix.
Traveltime perturbations may then be calculated from the wavefield
perturbation through a (linear) picking operator, 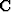 , such that
, such that
| 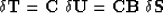 |
(6) |
where 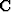 is a (linearized) picking operator, and a function
of the background wavefield, U0.
is a (linearized) picking operator, and a function
of the background wavefield, U0.
Cross-correlating the total wavefield, U(t), with U0(t), provides
a way of measuring their relative
time-shift, 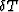 . Marquering et al. (1999) uses
this to provide the following explicit linear relationship between
. Marquering et al. (1999) uses
this to provide the following explicit linear relationship between
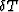 and
and 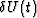 ,
,
| 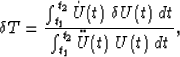 |
(7) |
where dots denote differentiation with respect to t, and t1 and
t2 define a temporal window around the event of interest.
Equation (7) is only valid for small time-shifts,
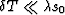 .
.





Next: Rytov traveltime sensitivity
Up: Theory
Previous: Theory
Stanford Exploration Project
4/27/2000
![]() , such that
, such that
![]() . Marquering et al. (1999) uses
this to provide the following explicit linear relationship between
. Marquering et al. (1999) uses
this to provide the following explicit linear relationship between
![]() and
and ![]() ,
,