ABSTRACT
For wave propagation at low frequencies in a porous medium,
the Gassmann-Domenico relations are well-established for homogeneous
partial saturation by a liquid. They provide the correct relations
for seismic velocities in terms of constituent
bulk and shear moduli, solid and fluid densities, porosity and
saturation. It has not been possible, however, to invert these
relations easily to determine porosity and saturation when the
seismic velocities are known. Also, the state (or distribution) of
saturation, i.e., whether or not liquid and gas are
homogeneously mixed in the pore space, is another important variable
for reservoir evaluation. A reliable ability to determine
the state of saturation from velocity data
continues to be problematic. We show how transforming
compressional and shear wave velocity data to the
(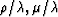 )-plane (where )-plane (where 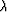 and and 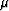 are the Lamé parameters and are the Lamé parameters and 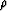 is the total density)
results in a set of quasi-orthogonal coordinates for porosity
and liquid saturation that greatly aids in the interpretation of
seismic data for the physical parameters of most interest.
A second transformation of the same data then permits isolation of the
liquid saturation value, and also provides some direct
information about the state of saturation.
By thus replotting the data
in the ( is the total density)
results in a set of quasi-orthogonal coordinates for porosity
and liquid saturation that greatly aids in the interpretation of
seismic data for the physical parameters of most interest.
A second transformation of the same data then permits isolation of the
liquid saturation value, and also provides some direct
information about the state of saturation.
By thus replotting the data
in the (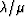 , , 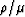 )-plane, inferences can be made
concerning the degree of patchy (inhomogeneous) versus homogeneous
saturation that is present in the region of the medium sampled by the data.
Our examples include igneous and sedimentary rocks, as well as
man-made porous materials. These results have potential applications
in various areas of interest, including petroleum exploration and
reservoir characterization, geothermal resource evaluation,
environmental restoration monitoring, and geotechnical site
characterization. )-plane, inferences can be made
concerning the degree of patchy (inhomogeneous) versus homogeneous
saturation that is present in the region of the medium sampled by the data.
Our examples include igneous and sedimentary rocks, as well as
man-made porous materials. These results have potential applications
in various areas of interest, including petroleum exploration and
reservoir characterization, geothermal resource evaluation,
environmental restoration monitoring, and geotechnical site
characterization.
|
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)