

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
SEP-103 -- TABLE OF CONTENTS
Velocity
Tau tomography with steering filters: 2-D field data example (ps.gz 2982K) (pdf 23813K) (src 13306K)
Clapp R. G. and Biondi B. L.
Common reflection point (CRP) gathers are usually parameterized in
terms of offset.
For tomography, a more convenient parameterization is in terms of
reflection angle.
Reflection angle CRP gathers can be constructed using wave equation migration.
By performing tomography in vertical travel-time (tau), focusing velocity,
rather than some combination of focusing and mapping velocity, can be
estimated.
By using anisotropic preconditioning
oriented along bedding planes, the solution can be guided towards
a geologically reasonable model.
The benefits of the tomography method are shown on
a 2-D line from a 3-D marine dataset.
Wave-equation migration velocity analysis: Episode II (ps.gz 2606K) (pdf 25490K) (src 30482K)
Sava P. and Biondi B.
We elaborate the main points of the wave-equation migration velocity analysis method introduced in a previous report. We analyze its strengths and limitations, and illustrate them using a synthetic example. The inversion results confirm our original expectations, especially with regard to stability and robustness. The main difficulty in recovering a complete velocity perturbation is related to the Born approximation, which limits the amount of residual migration improvement on the seismic images at any one given step.
Regularizing tomography with non-stationary filters (ps.gz 791K) (pdf 8030K) (src 192299K)
Clapp R. G.
The ideal regularizer is the inverse of the model covariance matrix.
Often the model covariance matrix has a complicated structure that is difficult
to characterize. Non-stationary prediction error filters (PEF)
have the ability to describe complicated model behavior.
Non-stationary filters are effective regularizers
for missing data and tomography problems.
Traveltime sensitivity kernels: Banana-doughnuts or just plain bananas? (ps.gz 66K) (pdf 408K) (src 77K)
Rickett J.
Estimating an accurate velocity function is one of the most critical
steps in building an accurate seismic depth image of the subsurface.
In areas with significant structural complexity, one-dimensional
updating schemes become unstable, and more robust algorithms are
needed.
Reflection tomography both in the premigrated Bishop et al. (1985) and
postmigrated domains Kosloff et al. (1996); Stork (1992) bring the powerful
...
Research interest: Improving the velocity model (ps.gz 210K) (pdf 788K) (src 473K)
Rosales D.
Travel time is perhaps one of the most important seismic parameter.
It can be used to
estimate properties of the subsurface. Velocity is one of these properties,
and its importance has been increasing because it is the unique
element that can convert time into depth. Seismic exploration has
been evolving from time studies to depth studies because they map actual
geology.
Velocities can be also used to estimate petrophysical properties.
...
Imaging
Stable wide-angle Fourier-finite difference downward extrapolation of 3-D wavefields (ps.gz 964K) (pdf 3097K) (src 1917K)
Biondi B.
I derive an unconditionally stable implicit finite-difference operator
that corrects the constant-velocity
phase shift operator for lateral velocity variations.
My method is based on the Fourier-Finite Difference (FFD) method first proposed
by Ristow and Ruhl 1994.
Contrary to previous results,
my correction operator is stable even when the reference velocity
is higher than the medium velocity.
Because of this additional capability,
after the correction step I can apply
a frequency-dependent interpolation
that significantly reduces:
the residual phase error after correction,
the frequency dispersion caused
by the discretization of the Laplacian operator,
and the azimuthal anisotropy caused by splitting.
Tests on zero-offset data from the
SEG-EAGE salt data set
show that the proposed method improves the imaging
of a fault reflection with respect to a similar interpolation
scheme that employs extended split-step to adapt to lateral velocity variations.
Efficient 3-D wavefield extrapolation with Fourier finite-differences and helical boundary conditions (ps.gz 188K) (pdf 424K) (src 419K)
Rickett J.
Fourier finite-difference (FFD) migration combines the
complementary advantages of the phase-shift and finite-difference
migration methods.
However, as with other implicit finite-difference algorithms, direct
application to 3-D problems is prohibitively expensive. Rather than
making the simple x-y splitting approximation that leads to
extensive azimuthal operator anisotropy, I demonstrate an alternative
approximation that retains azimuthal isotropy without the need for
additional correction terms.
Helical boundary conditions allow the critical 2-D inverse-filtering
step to be recast as 1-D inverse-filtering. A spectral factorization
algorithm can then factor this 1-D filter into a (minimum-phase)
causal component and a (maximum-phase) anti-causal component.
This factorization provides an LU decomposition of the matrix,
which can then be inverted directly by back-substitution.
The cost of this approximate inversion remains O(N) where N is the
size of the matrix.
Seismic image regularization in the reflection angle domain (ps.gz 157K) (pdf 3348K) (src 1519K)
Prucha M. L., Clapp R. G., and Biondi B.
We explore the use of preconditioned inversion in the reflection
angle domain rather than migration to improve imaging in complex
media. We use a wave-equation method to create reflection angle
domain common image gathers and we apply steering filter preconditioning
to smooth along the reflection angles. This improves the common
image gathers. The improved common image gathers are more continuous
than common image gathers obtained by migration alone. Additionally,
some multiple energy is attenuated.
Angle-gathers by Fourier Transform (ps.gz 1389K) (pdf 4620K) (src 8105K)
Sava P. and Fomel S.
In this paper, we present a method for computing angle-domain
common-image gathers from wave-equation depth-migrated seismic
images. We show that the method amounts to a radial-trace transform
in the Fourier domain and that it is equivalent to a slant stack in
the space domain. We obtain the angle-gathers using a stretch
technique that enables us to impose smoothness through
regularization. Several examples show that our method is accurate,
fast, robust, easy to implement and that it can be used for real
3-D prestack data in applications related to velocity analysis and
amplitude-versus angle (AVA) analysis.
Spectral factorization of 2-D reflection seismic data (ps.gz 162K) (pdf 587K) (src 151K)
Claerbout J.
I propose spectral factorization of 2-D seismic data.
Boulders strewn on the water bottom of an otherwise
horizontally layered earth
imply that the multidimensional minimum-phase wavelet of
a zero-offset section
is a common midpoint gather.
Common-azimuth migration and Kirchhoff migration for 3-D prestack imaging: A comparison on North Sea data (ps.gz 4287K) (pdf 8294K) (src 16196K)
Vaillant L. and Calandra H.
Common-azimuth migration (CAM) is a 3-D
prestack depth migration technique based on the wave equation
Biondi and Palacharla (1996). It exploits the intrinsic narrow-azimuth nature of
marine data to reduce its dimensionality and thus manages to cut the
computational cost of 3-D imaging significantly enough to compete with
Kirchhoff methods. Based on a recursive
extrapolation of the recorded wavefield, CAM is potentially better
able to handle multi-pathing problems induced by complex velocity
structures.
...
Variable-velocity prestack Stolt residual migration with application to a North Sea dataset (ps.gz 2439K) (pdf 5477K) (src 32734K)
Sava P.
This paper investigates the applicability of prestack Stolt residual migration when the original image is obtained using an arbitrary velocity model. At its origin, the method is based on an assumption of constant velocity. However, its formulation for depth-migrated images involves a ratio of the reference and target velocities; therefore, for residual migration it is completely irrelevant if the original migration uses constant or variable velocity. Several examples, both on synthetic and real data demonstrate the effectiveness of the method. When applied to a North Sea dataset, the method highlights important features not seen in the original migration.
Accuracy of common-azimuth migration approximations (ps.gz 405K) (pdf 6644K) (src 643188K)
Vaillant L. and Biondi B.
Common-azimuth migration (CAM) is an attractive solution for 3-D
prestack imaging. It reduces the full 5-D phase-shift operator to 4-D
through the stationary-phase approximation, lowering the computational
cost. However, this assumption yields constraints in the
downward-continuation process that can limit accuracy. Those errors
are estimated in this paper by comparison to other wave-equation
methods and to analytical solutions. Common-azimuth migration appears
robust, but leaves opportunities for formulating an extended migration
algorithm, which overcomes some of its inherent limits.
Sub-salt imaging of a 2-D elastic synthetic model, using prestack, split-step, wave equation migration (ps.gz 2902K) (pdf 23910K) (src 5197K)
Gratwick D.
This paper explores methods to image complex structures under a salt body, using
a 2-D elastic synthetic model. The modeling algorithm handles complex features such as
energy from multiple reflections and mode conversion.
I show that a complex wave equation depth migration algorithm is needed to
position the salt boundaries and reflectors from sediments below the salt properly.
Also, using
simple ray-tracing diagrams, I show that energy from converted waves is useful in
imaging steeply dipping reflectors below the salt.
Though these techniques improve overall image quality,
parts of the image under the salt are still left unresolved, and I outline possible techniques for
imaging these reflectors.
Coherent noise
Prestack multiple attenuation using the hyperbolic Radon transform (ps.gz 5087K) (pdf 10300K) (src 10525K)
Guitton A.
I apply the iterative hyperbolic Radon transform to CMP gathers to create
a velocity panel where multiples and primaries are separable. The velocity panel
is created using three different inversion schemes: (1) l2 norm inversion,
(2) l1 norm inversion and (3) l1 norm with l1 regularization inversion.
The third technique is particularly efficient at separating primaries and
multiples in the prestack domain. A comparison of the three techniques shows that
some noticeable differences appear in the prestack domain after multiple attenuation
and that no discrepancies emerge on the stacked sections. These conclusions
are linked to convergence properties of each method, and also linked to the
``quality'' of the data.
(t-x) domain, pattern-based multiple separation (ps.gz 627K) (pdf 2866K) (src 4568K)
Clapp R. G. and Brown M.
Pattern-based signal/noise separation is a common technique to
suppress multiples.
It can be formulated in the t-x domain using non-stationary
Prediction Error Filters (PEF).
One can obtain a kinematically correct model of the multiples by
downward continuation. The CMP gather and the
corresponding multiple estimate are characterized by
a space varying PEF.
After applying a simple separation technique one can obtain
CMP gathers where the multiple energy is significantly attenuated.
The method is applied to synthetic and 2-D field CMP gathers.
Spitz makes a better assumption for the signal PEF (ps.gz 49K) (pdf 596K) (src 83K)
Claerbout J. and Fomel S.
In real-world extraction of signal from data
we are not given the needed signal prediction-error filter (PEF).
Claerbout has taken S, the PEF of the signal,
to be that of the data, 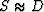 . Spitz takes it to be
. Spitz takes it to be 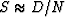 . Where noises are highly predictable in time or space,
Spitz gets significantly better results.
Theoretically, a reason is that the essential character
of a PEF is contained where it is small.
. Where noises are highly predictable in time or space,
Spitz gets significantly better results.
Theoretically, a reason is that the essential character
of a PEF is contained where it is small.
Ground roll and the Radial Trace Transform - revisited (ps.gz 1680K) (pdf 9761K) (src 5356K)
Brown M. and Claerbout J.
The Radial Trace Transform (RTT) is an attractive tool for wavefield separation
because it lowers the apparent temporal frequency of radial events like ground roll,
making it possible to remove them from the data by simple bandpass filtering in the
Radial Trace (RT) domain. We discuss two implementations of the RTT. In the first,
and better known, the RT domain is well-sampled, and thus suitable for post-filtering,
but is prone to interpolation errors. We present an alternate implementation, which is
pseudo-unitary in the limit of an infinitely densely sampled RT space, with the side
effect that the RT domain has missing data. Using a simple 2-D filter for
regularization, we estimate the missing data in the RT domain by least squares
optimization, without affecting the invertibility of the RTT.
Our implementation suppresses radial noise while preserving signal, including static
shifts. Although it runs into trouble when noise is spatially aliased, we show that
application of a linear moveout correction prior to processing increases our scheme's
effectiveness.
Optimization
Seismic data interpolation with the offset continuation equation (ps.gz 1342K) (pdf 8120K) (src 4487K)
Fomel S.
I propose a finite-difference offset continuation filter for
interpolating seismic reflection data. The filter is constructed
from the offset continuation differential equation and is applied on
frequency slices in the log-stretch frequency domain. Synthetic data
tests produce encouraging results: nearly perfect interpolation of a
constant-velocity dataset with a complex reflector model and
reasonably good interpolation of the Marmousi dataset.
Huber solver versus IRLS algorithm for quasi L1 inversion (ps.gz 396K) (pdf 3470K) (src 1059K)
Guitton A.
The l1 problem can be approximated using either Iteratively Reweighted Least
Squares methods (IRLS) with an appropriate weighting function or the Huber
misfit function with an appropriate solver. Comparisons of both methods
show that they give very similar results as they handle problems suited to l1 properly.
In addition, the nonlinear scheme, using the Huber norm, generally converges better than
the linear IRLS algorithms on velocity-stack inversion. Finally, the Huber solver is far
easier to operate because it is sensitive to fewer parameters than IRLS.
Speculations on contouring sparse data: Gaussian curvature (ps.gz 29K) (pdf 192K) (src 10K)
Claerbout J. and Fomel S.
We speculate about regularizing (interpolating) sparse data.
We speculate that L1 regularization would be desirable.
An example convinces us it would not.
Changing direction we learn that
flexed paper has zero Gaussian curvature.
Unfortunately, Gaussian curvature
is a nonlinear function of the altitude.
Implementation of a nonlinear solver for minimizing the Huber norm (ps.gz 30K) (pdf 211K) (src 8K)
Guitton A.
The Huber norm Huber (1973) is an alternative to Iteratively Reweighted Least Square
programs for solving the hybrid l2-l1 problem. In this note, I detail a method for
minimizing the Huber norm.
Because the Huber norm gives rise to a non-linear problem with non-twice continuously differentiable
objective functions, its use is quite challenging. Claerbout (1996) implemented
a Huber regression based on conjugate-gradient descents. However, the final results were not satisfying.
Here I propose to solve the Huber problem using a quasi-Newton update of the solution with
the computation of an approximated Hessian (second derivative of the objective function).
...
Helix filtering
Helical preconditioning and splines in tension (ps.gz 1378K) (pdf 5070K) (src 3964K)
Fomel S.
Splines in tension are smooth interpolation surfaces whose
behavior in unconstrained regions is controlled by the tension
parameter. I show that such surfaces can be efficiently constructed
with recursive filter preconditioning and introduce a family of
corresponding two-dimensional minimum-phase filters. The filters are
created by spectral factorization on a helix.
Patching and micropatching in seismic data interpolation (ps.gz 201K) (pdf 3911K) (src 13175K)
Crawley S.
I interpolate CMP gathers with PEFs arranged on a dense, radial grid.
The radial grid facilitates preconditioning by radial smoothing,
and enables the use of relatively large grid cells, which
we refer to as micropatches.
Even when the micropatches contain enough data samples that
the PEF calculation problem appears overdetermined, radial smoothing
still noticeably improves the interpolation, particularly on noisy data.
The Burg Method on a Helix? (ps.gz 14K) (pdf 61K) (src 5K)
Claerbout J.
Burg PEF estimation should work fine on a helix.
Full details along with the 1-D code
are found at Claerbout (1976).
I will quickly review the theory from memory
(partly to see how simple I can make it).
First is the notion that PEFs can be built up
from this recursion
...
Data alignment with non-stationary shaping filters (ps.gz 521K) (pdf 5844K) (src 984K)
Rickett J.
Cross-correlation provides a method of calculating a static shift
between two datasets. By cross-correlating patches of data, I can
calculate a ``warp function'' that dynamically aligns the two
datasets.
By exploiting the link between cross-correlation and shaping filters,
I calculate warp functions in a more general way, leveraging
the full machinery of geophysical estimation.
I compare warp functions, derived by the two methods, for simple one
and two-dimensional applications. For the one-dimensional well-tie
example, shaping filters gave significantly improved results; however,
for the two dimensional residual migration example, the
cross-correlation technique gave the better results.
I also explain how the helical transform allows the problem of finding
a shaping filter to be formulated as an auto-regression.
Random lines in a plane (ps.gz 55K) (pdf 709K) (src 105K)
Claerbout J.
Locally, seismic data is a superposition of plane waves.
The statistical properties of such superpositions
are relevant to geophysical estimation
and they are not entirely obvious.
Clearly, a planar wave can be constructed from a planar
distribution of point sources.
Contrariwise, a point source can be constructed from
a superposition of plane waves going in all directions.
...
Test case for PEF estimation with sparse data (ps.gz 12K) (pdf 33K) (src 4K)
Claerbout J.
We begin with a rough one-dimensional function.
A random walk would be nice,
the integral of random numbers (possibly coin flips).
Call it r(x).
Actually, I'd like a random walk that crosses the zero axis
a couple times. We could try several seeds until we find
an "attractive" one.
Maybe leaky integrate random numbers.
Next, flex a piece of paper so that along the x-axis
...
Reservoir characterization
Transformation of seismic velocity data to extract porosity and saturation values for rocks (ps.gz 70K) (pdf 1862K) (src 174K)
Berryman J. G., Berge P. A., and Bonner B. P.
For wave propagation at low frequencies in a porous medium,
the Gassmann-Domenico relations are well-established for homogeneous
partial saturation by a liquid. They provide the correct relations
for seismic velocities in terms of constituent
bulk and shear moduli, solid and fluid densities, porosity and
saturation. It has not been possible, however, to invert these
relations easily to determine porosity and saturation when the
seismic velocities are known. Also, the state (or distribution) of
saturation, i.e., whether or not liquid and gas are
homogeneously mixed in the pore space, is another important variable
for reservoir evaluation. A reliable ability to determine
the state of saturation from velocity data
continues to be problematic. We show how transforming
compressional and shear wave velocity data to the
(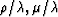 )-plane (where
)-plane (where 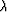 and
and 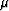 are the Lamé parameters and
are the Lamé parameters and 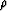 is the total density)
results in a set of quasi-orthogonal coordinates for porosity
and liquid saturation that greatly aids in the interpretation of
seismic data for the physical parameters of most interest.
A second transformation of the same data then permits isolation of the
liquid saturation value, and also provides some direct
information about the state of saturation.
By thus replotting the data
in the (
is the total density)
results in a set of quasi-orthogonal coordinates for porosity
and liquid saturation that greatly aids in the interpretation of
seismic data for the physical parameters of most interest.
A second transformation of the same data then permits isolation of the
liquid saturation value, and also provides some direct
information about the state of saturation.
By thus replotting the data
in the (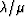 ,
, 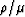 )-plane, inferences can be made
concerning the degree of patchy (inhomogeneous) versus homogeneous
saturation that is present in the region of the medium sampled by the data.
Our examples include igneous and sedimentary rocks, as well as
man-made porous materials. These results have potential applications
in various areas of interest, including petroleum exploration and
reservoir characterization, geothermal resource evaluation,
environmental restoration monitoring, and geotechnical site
characterization.
)-plane, inferences can be made
concerning the degree of patchy (inhomogeneous) versus homogeneous
saturation that is present in the region of the medium sampled by the data.
Our examples include igneous and sedimentary rocks, as well as
man-made porous materials. These results have potential applications
in various areas of interest, including petroleum exploration and
reservoir characterization, geothermal resource evaluation,
environmental restoration monitoring, and geotechnical site
characterization.
Estimation of AVO attributes sensitivity to velocity uncertainty using forward modeling: a progress report (ps.gz 802K) (pdf 10347K) (src 1414K)
Mora C. and Biondi B.
We investigate the sensitivity of AVO attributes to
uncertainty in migration velocity in a synthetic dataset.
The synthetic data was built using a earth model with typical rock properties
from a real North Sea turbidite field.
The model includes a thick overburden layer with complex
velocity anomalies.
We examine the sensitivity of AVO response due to the presence
of this complex layer and quantify the influence of migration velocity
errors in the AVO signature.
Results show that AVO gradient attribute is more sensitive to
velocity errors than AVO intercept attribute.
For velocity errors up to 5% we see a maximum of AVO intercept errors
of 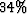 , whereas for velocity errors of only 1%, the inversion of
AVO gradient attribute has an error of 185%.
Further work is needed to evaluate the influence of observed boundary artifacts
on these results.
, whereas for velocity errors of only 1%, the inversion of
AVO gradient attribute has an error of 185%.
Further work is needed to evaluate the influence of observed boundary artifacts
on these results.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
4/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)