




Next: Acknowledgments
Up: Claerbout & Fomel: Estimating
Previous: BASIC THEORY
We assume that the data vector 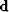 is composed of the signal
and noise components
is composed of the signal
and noise components  and
and 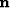 :
:
| 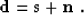 |
(5) |
If both the signal and noise prediction-error filters S and
N are known, then the signal can be extracted from the data
by solving the following system by the least squares method:
| 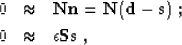 |
(6) |
| (7) |
where  is a scalar scaling coefficient, reflecting the
presumed signal-to-noise ration Claerbout (1999).
is a scalar scaling coefficient, reflecting the
presumed signal-to-noise ration Claerbout (1999).
The formal solution of system (6-7)
has the form of a projection filter :
| 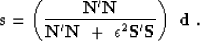 |
(8) |
Analogously, the signal vector is expressed as
| 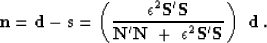 |
(9) |
In 1-D or F-X setting, one can accomplish the division in
formulas (8) and (9) directly by
spectral factorization and inverse recursive filtering
Soubaras (1994, 1995). A similar approach can be applied
in the case of T-X or F-XY filtering with the help of the
helix transform Claerbout (1998); Ozdemir et al. (1999) or by
solving system (6-7) directly with
an iterative method Abma (1995).
Claerbout's approach, implemented in the examples of GEE
Claerbout (1999), is to estimate the signal and noise PEFs S and N from
the data  by specifying different shape templates for these
two filters. The filter estimates can be iteratively refined after the
initial signal and noise separation. In some examples, such as those
shown in this paper, the signal and noise templates are not easily
separated. When the signal template behaves as an extension of the
noise template so that the shape of S completely embeds the shape of
N, our estimate of S serves as a predictor of both signal and
noise. We might as well consider it as D, the prediction-error
filter for the data.
by specifying different shape templates for these
two filters. The filter estimates can be iteratively refined after the
initial signal and noise separation. In some examples, such as those
shown in this paper, the signal and noise templates are not easily
separated. When the signal template behaves as an extension of the
noise template so that the shape of S completely embeds the shape of
N, our estimate of S serves as a predictor of both signal and
noise. We might as well consider it as D, the prediction-error
filter for the data.
Spitz (1999) argues that the data PEF D can
be regarded as the convolution of the signal and noise PEFs
S and N.
This assertion suggests the following
algorithm:
- 1.
- Estimate D and N.
- 2.
- Estimate S by deconvolving (polynomial division)
D by N.
- 3.
- Solve the least-square system (6-7).
To avoid the division step, we suggest a simple modification of
Spitz's algorithm, which results from multiplying both equations in
system (6-7) by the noise
filtering operator  . The resulting system has the form
. The resulting system has the form
| 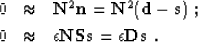 |
(10) |
| (11) |
The modified algorithm is
- 1.
- Estimate D and N.
- 2.
- Convolve N with itself.
- 3.
- Solve the least-square system (10-11).
The formal least-squares solution of
system (10-11) is
| 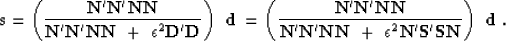 |
(12) |
Comparing (12) with (8), we can see
that both the numerator and the denominator in the two expressions
differ by the same multiplier 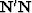 . This multiplication
should not effect the result of projection filtering.
. This multiplication
should not effect the result of projection filtering.
Figure 1 shows a simple example of signal and noise
separation taken from GEE Claerbout (1999). The signal consists of
two crossing plane waves with random amplitudes, and the noise is
spatially random. The data and noise T-X prediction-error filters
were estimated from the same data by applying different filter
templates. The template for D is
a a
a a
a a
1 a a
a a a
a a a
a a a
where the a symbol represents adjustable coefficients. The
data filter shape has three columns, which allows it to predict two
plane waves with different slopes. The noise filter N has
only one column. Its template is
1
a
a
a
The noise PEF can estimate the temporal spectrum but would fail to
capture the signal predictability in the space direction.
Figure 2 shows the result of applying the modified
Spitz method according to
equations (10-11).
Comparing
figures 1 and 2,
we can see that using
a modified system of equations brings
a slightly modified result with more noise in the signal
but more signal in the noise.
It is as if  has changed,
and indeed this could be the principal effect
of neglecting the denominator in equation (3).
signoi90
has changed,
and indeed this could be the principal effect
of neglecting the denominator in equation (3).
signoi90
Figure 1 Signal and noise separation with the
original GEE method. The input signal is on the left. Next is that
signal with random noise added. Next are the estimated signal and
the estimated noise.




 signoi
signoi
Figure 2 Signal and noise separation
with the modified Spitz method. The input signal is on the left.
Next is that signal with random noise added. Next are the estimated signal
and the estimated noise.





To illustrate a significantly different result
using the Spitz insight we examine the new situation shown in
Figures 3 and 4.
The wave with the positive slope is considered to be
regular noise;
the other wave is signal.
The noise PEF N was
estimated from the data by restricting the filter shape so that it
could predict only positive slopes. The corresponding template is
a
1 a
The data PEF template is
a a
a a
1 a a
a a a
a a a
Using the data PEF as a substitute for the signal PEF produces a poor
result, shown in Figure 3. We see a part of the
signal sneaking into the noise estimate. Using the modified Spitz
method, we obtain a clean separation of the plane waves
(Figure 4).
planes90
Figure 3 Plane wave separation with the
GEE method. The input signal is on the left. Next is that signal
with noise added. Next are the estimated signal and the estimated
noise.




 planes
planes
Figure 4 Plane wave separation with the
modified Spitz method. The input signal is on the left. Next is
that signal with noise added. Next are the estimated signal and the
estimated noise.





Clapp and Brown (1999, 2000) and
Brown et al. (1999) show applications of the
least-squares signal-noise separation to multiple and ground-roll
elimination.





Next: Acknowledgments
Up: Claerbout & Fomel: Estimating
Previous: BASIC THEORY
Stanford Exploration Project
4/27/2000
![]() is composed of the signal
and noise components
is composed of the signal
and noise components ![]() and
and ![]() :
:
![]() by specifying different shape templates for these
two filters. The filter estimates can be iteratively refined after the
initial signal and noise separation. In some examples, such as those
shown in this paper, the signal and noise templates are not easily
separated. When the signal template behaves as an extension of the
noise template so that the shape of S completely embeds the shape of
N, our estimate of S serves as a predictor of both signal and
noise. We might as well consider it as D, the prediction-error
filter for the data.
by specifying different shape templates for these
two filters. The filter estimates can be iteratively refined after the
initial signal and noise separation. In some examples, such as those
shown in this paper, the signal and noise templates are not easily
separated. When the signal template behaves as an extension of the
noise template so that the shape of S completely embeds the shape of
N, our estimate of S serves as a predictor of both signal and
noise. We might as well consider it as D, the prediction-error
filter for the data.



