Slowness inversion

Once we have created an image perturbation , we can invert for the corresponding perturbation in slowness. Mathematically, this amounts to solving an optimization problem like Claerbout (1999)

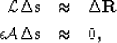$$\begin{eqnarray} \mathcal L\Delta \bf s&\approx& \Delta{\bf R}\\ \nonumber \epsilon\mathcal A\Delta \bf s&\approx& 0,\end{eqnarray}$$ (1)

where

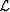• $\mathcal L$ is a data-fitting operator, mainly composed of a scattering and a downward continuation operator, but which also incorporates the background wavefield Biondi and Sava (1999),
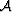• $\mathcal A$ is a model-styling operator, either an isotropic Laplacian or an anisotropic steering-filter Clapp and Biondi (1998), which imposes smoothing on the model,
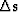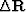• $\Delta \bf s$ and $\Delta{\bf R}$ are respectively the slowness perturbation (the model) and the image perturbation (the data),
• $\epsilon$ is a scalar parameter controlling the weight of each of the individual goals.

To speed-up the inversion procedure, we can precondition the model in Equation 1 and solve the system

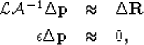$$\begin{eqnarray} \mathcal L\mathcal A^{-1}\Delta{\bf p}&\approx& \Delta{\bf R}\\ \nonumber \epsilon\Delta{\bf p}&\approx& 0,\end{eqnarray}$$ (2)

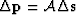where $\Delta{\bf p}=\mathcal A\Delta \bf s$ is the preconditioned model variable.