




Next: Results
Up: Proposed solutions to attenuate
Previous: METHOD 1: A filtering
Instead of removing the noise by filtering, we can remove it
by subtraction. If an operator
is unable to model all the information embedded in the data, then the residual is not IID.
The second formulation I propose is based on the idea that
if we can model the coherent noise with another operator, then the residual components
become IID.
Let us consider that we have
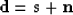
and that there exists an operator L such that
![\begin{displaymath}
{\bf L}=[{\bf H}\;\;\; {\bf L_n}].\end{displaymath}](img28.gif)
We assume that H is the modeling operator for the
signal s and that 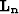 is the modeling operator
for the coherent noise n. Following this decomposition, we can write
is the modeling operator
for the coherent noise n. Following this decomposition, we can write
![\begin{displaymath}
{\bf m}=\left [ \begin{array}
{c}
{\bf m_s}\ {\bf m_n}
\end{array} \right ]\end{displaymath}](img30.gif)
where 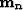 is the noise-model and
is the noise-model and 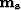 is the
signal-model.
Starting from
is the
signal-model.
Starting from
| 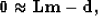 |
(12) |
the fitting goal then becomes
| 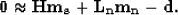 |
(13) |
Because we have to find 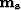 and
and 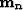 ,
this system is clearly under-determined and some regularization is needed.
Thus, we end up with the following fitting goals
Because there should be a different operator
,
this system is clearly under-determined and some regularization is needed.
Thus, we end up with the following fitting goals
Because there should be a different operator 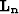 for each
different coherent noise pattern, the cost of this method increases
considerably.
Fortunately, we can use multi-dimensional PEFs to estimate the coherent noise operator.
This estimation is possible if we assume that the coherent noise
is predictable, i.e., made up of the superposition of local plane
wave segments Claerbout (1992). If we can
estimate PEFs from the coherent noise, then the inverse PEF should
be our coherent noise modeling operator
for each
different coherent noise pattern, the cost of this method increases
considerably.
Fortunately, we can use multi-dimensional PEFs to estimate the coherent noise operator.
This estimation is possible if we assume that the coherent noise
is predictable, i.e., made up of the superposition of local plane
wave segments Claerbout (1992). If we can
estimate PEFs from the coherent noise, then the inverse PEF should
be our coherent noise modeling operator 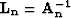 .
Computing the inverse of multi-dimensional PEFs is now possible via
the helix. In addition, with the helical boundary conditions, computing the inverse
of multi-dimensional PEFs is as easy as computing the inverse of 1-D filters. We have then
.
Computing the inverse of multi-dimensional PEFs is now possible via
the helix. In addition, with the helical boundary conditions, computing the inverse
of multi-dimensional PEFs is as easy as computing the inverse of 1-D filters. We have then
| 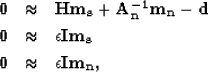 |
|
| (14) |
| |
where 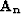 is the noise PEF. This approach is
similar to Tamas Nemeth's approach 1996.
The difference emerges in the choice of the operators
is the noise PEF. This approach is
similar to Tamas Nemeth's approach 1996.
The difference emerges in the choice of the operators
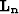 and
and 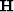 . Whereas Nemeth (1996) imposes one operator
. Whereas Nemeth (1996) imposes one operator
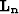 to model the noise, we estimate a PEF
to model the noise, we estimate a PEF 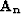 and use
it in the fitting goals (Equation 15). Because PEFs
(with appropriate dimensions) whiten the spectrum of many different plane-waves,
this strategy is more flexible (no assumptions regarding the moveout of the noise).
This method should give IID residual variables as long as we are able
to estimate PEFs for the coherent noise. This is the main difficulty and challenge
of this method. The minimization of the objective function in a least-squares sense
for the fitting goals in Equation 15 can be done again with a fast conjugate
gradients method.
and use
it in the fitting goals (Equation 15). Because PEFs
(with appropriate dimensions) whiten the spectrum of many different plane-waves,
this strategy is more flexible (no assumptions regarding the moveout of the noise).
This method should give IID residual variables as long as we are able
to estimate PEFs for the coherent noise. This is the main difficulty and challenge
of this method. The minimization of the objective function in a least-squares sense
for the fitting goals in Equation 15 can be done again with a fast conjugate
gradients method.
I did not develop any specific algorithm to solve this inverse problem. I assume
that we have a strategy that allows us to estimate the operator 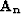 .
We can then minimize the objective function for the fitting goals given in Equation 15
in a least-squares sense, for example.
.
We can then minimize the objective function for the fitting goals given in Equation 15
in a least-squares sense, for example.





Next: Results
Up: Proposed solutions to attenuate
Previous: METHOD 1: A filtering
Stanford Exploration Project
9/5/2000
![]()
![]()
![]()
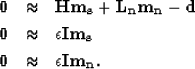
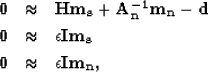
![]() .
We can then minimize the objective function for the fitting goals given in Equation 15
in a least-squares sense, for example.
.
We can then minimize the objective function for the fitting goals given in Equation 15
in a least-squares sense, for example.