Unser et al. (1993) noticed that the basis function idea has an especially simple implementation if the basis is convolutional and satisfies the equation
| |
(65) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into
equation (
) into
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields
) yields
| |
(66) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) at an
integer value n, we obtain the equation
) at an
integer value n, we obtain the equation
| |
(67) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to obtain the
coefficients ck from f(n) by inverse recursive filtering
(deconvolution). In the case of a non-causal filter
) to obtain the
coefficients ck from f(n) by inverse recursive filtering
(deconvolution). In the case of a non-causal filter
According to the convolutional basis idea, forward interpolation
becomes a two-step procedure. The first step is the direct inversion
of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ): the basis coefficients ck are found by
deconvolving the sampled function f(n) with the factorized filter
): the basis coefficients ck are found by
deconvolving the sampled function f(n) with the factorized filter
![]() . The second step reconstructs the continuous (or arbitrarily
sampled) function f(x) according to formula (
. The second step reconstructs the continuous (or arbitrarily
sampled) function f(x) according to formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
two steps could be combined into one, but usually it is more
convenient to apply them separately. I show a schematic relationship
among different variables in Figure
). The
two steps could be combined into one, but usually it is more
convenient to apply them separately. I show a schematic relationship
among different variables in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
|
scheme
Figure 12 Schematic relationship among different variables for interpolation with a convolutional basis. | 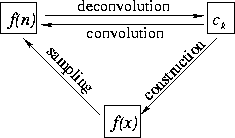 |