




Next: Solving the Cauchy problem
Up: Three-dimensional seismic data regularization
Previous: Conclusions
Second-order reflection traveltime derivatives
In this appendix, I derive equations connecting second-order partial
derivatives of the reflection traveltime with the geometric properties
of the reflector in a constant velocity medium. These equations are
used in the main text of Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for the amplitude
behavior description. Let
for the amplitude
behavior description. Let 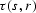 be the reflection traveltime
from the source s to the receiver r. Consider a formal equality
be the reflection traveltime
from the source s to the receiver r. Consider a formal equality
| 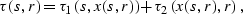 |
(266) |
where x is the reflection point parameter, 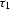 corresponds to the
incident ray, and
corresponds to the
incident ray, and 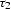 corresponds to the reflected ray.
Differentiating (
corresponds to the reflected ray.
Differentiating (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to s and r yields
) with respect to s and r yields
| 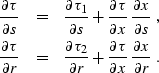 |
(267) |
| (268) |
According to Fermat's principle, the two-point reflection ray path must
correspond to the traveltime stationary point. Therefore
| 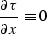 |
(269) |
for any s and r. Taking into account (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) while
differentiating (
) while
differentiating (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we get
), we get
| 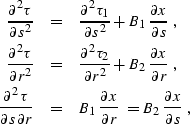 |
(270) |
| (271) |
| (272) |
where
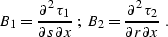
Differentiating equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) gives us the additional
pair of equations
) gives us the additional
pair of equations
| 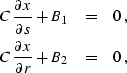 |
(273) |
| (274) |
where
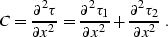
Solving the system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) - (
) - (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for
) for 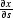 and
and 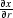 and substituting
the result into (
and substituting
the result into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) - (
) - (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) produces the
following set of expressions:
) produces the
following set of expressions:
| 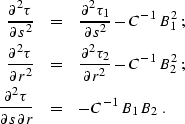 |
(275) |
| (276) |
| (277) |
In the case of a constant velocity medium, expressions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to
(
) to
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be applied directly to the explicit
equation for the two-point eikonal
) can be applied directly to the explicit
equation for the two-point eikonal
| 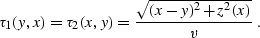 |
(278) |
Differentiating (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and taking into account the trigonometric
relationships for the incident and reflected rays (Figure
) and taking into account the trigonometric
relationships for the incident and reflected rays (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), one can
evaluate all the quantities in (
), one can
evaluate all the quantities in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to (
) to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) explicitly.
After some heavy algebra, the resultant expressions for the traveltime
derivatives take the form
) explicitly.
After some heavy algebra, the resultant expressions for the traveltime
derivatives take the form
| 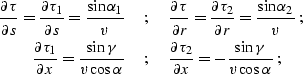 |
(279) |
| (280) |
| 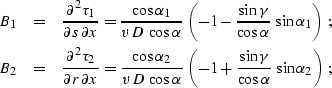 |
(281) |
| (282) |
| 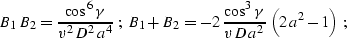 |
(283) |
| 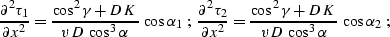 |
(284) |
| 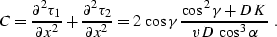 |
(285) |
Here D is the length of the normal (central) ray,  is its dip angle
(
is its dip angle
(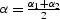 ,
, 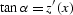 ),
),
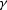 is the reflection angle
is the reflection angle
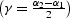 , K is the reflector
curvature at the reflection point
, K is the reflector
curvature at the reflection point 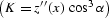 , and
a is the dimensionless function of
, and
a is the dimensionless function of  and
and 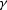 defined in (
defined in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
The equations derived in this appendix were used to get the equation
| 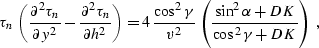 |
(286) |
which coincides with (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the main text.
) in the main text.





Next: Solving the Cauchy problem
Up: Three-dimensional seismic data regularization
Previous: Conclusions
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for the amplitude
behavior description. Let
for the amplitude
behavior description. Let ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to s and r yields
) with respect to s and r yields
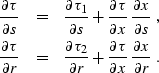
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) while
differentiating (
) while
differentiating (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we get
), we get
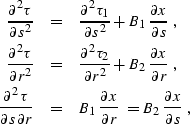
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) gives us the additional
pair of equations
) gives us the additional
pair of equations
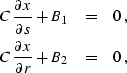
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) - (
) - (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for
) for ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) - (
) - (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) produces the
following set of expressions:
) produces the
following set of expressions:
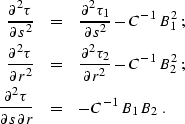
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to
(
) to
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be applied directly to the explicit
equation for the two-point eikonal
) can be applied directly to the explicit
equation for the two-point eikonal
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and taking into account the trigonometric
relationships for the incident and reflected rays (Figure
) and taking into account the trigonometric
relationships for the incident and reflected rays (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), one can
evaluate all the quantities in (
), one can
evaluate all the quantities in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to (
) to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) explicitly.
After some heavy algebra, the resultant expressions for the traveltime
derivatives take the form
) explicitly.
After some heavy algebra, the resultant expressions for the traveltime
derivatives take the form
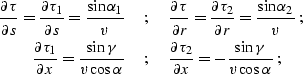
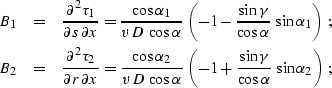
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the main text.
) in the main text.