




Next: Model Variability
Up: R. Clapp: Multiple realizations
Previous: R. Clapp: Multiple realizations
Inverse problems obtain an estimate of
a model 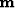 , given some data
, given some data 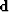 and an
operator
and an
operator 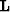 relating the two.
We can write our estimate of
the model as minimizing the
objective function
in a least-squares sense,
relating the two.
We can write our estimate of
the model as minimizing the
objective function
in a least-squares sense,
| 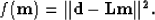 |
(1) |
We can think of this same minimization in terms of fitting goals
as
| 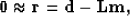 |
(2) |
where  is a residual vector.
is a residual vector.
Bayesian theory tells us Tarantola (1987) that convergence rate and
the final quality of the model is improved the closer  is
to being Independent Identically Distributed (IID).
If we include the inverse noise covariance
is
to being Independent Identically Distributed (IID).
If we include the inverse noise covariance 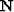 in
our inversion our residual beomes IID,
in
our inversion our residual beomes IID,
| 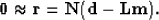 |
(3) |
A regularized inversion problem can be thought of
as a more complicated version of (3) with
an expanded data vector and an additional covariance operator,
|  |
|
| (4) |
In this new formulation
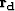
- is the residual from the data fitting goal,
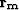
- is the residual from the model styling goal,
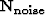
- is the inverse noise covariance,
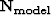
- is the inverse model covariance,
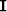
- is the identity matrix, and

- is a scalar that balances the fitting goals
against each other.
Normally we think of 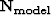 as the regularization
operator
as the regularization
operator 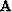 . Simple linear algebra leads to a more
standard set of fitting goals:
. Simple linear algebra leads to a more
standard set of fitting goals:
| 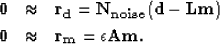 |
|
| (5) |
The problem with this approach is that we never know the
true inverse noise or model covariance and therefore are only capable
of applying approximate forms of these matrices.





Next: Model Variability
Up: R. Clapp: Multiple realizations
Previous: R. Clapp: Multiple realizations
Stanford Exploration Project
7/8/2003
![]() is
to being Independent Identically Distributed (IID).
If we include the inverse noise covariance
is
to being Independent Identically Distributed (IID).
If we include the inverse noise covariance ![]() in
our inversion our residual beomes IID,
in
our inversion our residual beomes IID,